例如,在图中,三条长度均为L的绳子共同系住一个密度均匀的小球m,球直径为d。若摆球在纸面内做小角度的左右摆动,摆动圆弧的圆心在O1处,故等效摆长为
如图所示,甲为某一简谐横波在t=1.0s时刻的图象,乙为参与波动的某一质点的振动图象。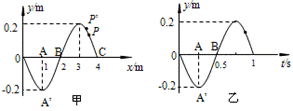
(1)两图中的AA’、OC各表示什么物理量?量值各是多少?
(2)说明两图中OA ’B段图线的意义?
(3)该波的波速为多大?
(4)画出再经过0.25s后的波动图象和振动图象。
(5)甲图中P点此刻的振动方向。
利用超声波可以探测鱼群的位置。在一只装有超声波发射和接收装置的渔船上,向选定的方向发射出频率f=5.8×104Hz的超声波后,经过时间t=0.64s收到从鱼群反射回来的反射波。已知这列超声波在水中的波长λ=2.5cm,求鱼群到渔船的距离是多少?
利用超声波测量汽车的速度,超声波遇到障碍物会发生反射,测速仪发出并接收反射回来的超声波脉冲信号,根据发出和接收到的时间差,测出汽车的速度。图30(a)是在高速公路上用超声波测速仪测量车速的示意图,测速仪发出并接收超声波脉冲信号,根据发出和接收到的时间差,测出汽车的速度。图30(b)中是测速仪发出的超声波信号,n1、n2分别是由汽车反射回来的信号。设测速仪匀速扫描,p1、、p2之间的时间间隔Δt=1.0s,超声波在空气中传播的速度是V=340m。/s,若汽车是匀速行驶的,则根据图(b)可知,汽车在接收到p1、、p2两个信号之间的时间内前进的距离___m,汽车的速度是_____________m/s 
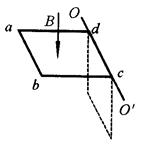
如图所示,由粗细相同的导线制成的正方形线框边长为L,每条边的电阻均为R,其中ab边材料的密度较大,其质量为m,其余各边的质量均可忽略不计.线框可绕与cd边重合的水平轴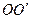 自由转动,不计空气阻力及摩擦.若线框从水平位置由静止释放,经历时间t到达竖直位置,此时ab边的速度大小为v.若线框始终处在方向竖直向下、磁感强度为B的匀强磁场中,重力加速度为g.求:
自由转动,不计空气阻力及摩擦.若线框从水平位置由静止释放,经历时间t到达竖直位置,此时ab边的速度大小为v.若线框始终处在方向竖直向下、磁感强度为B的匀强磁场中,重力加速度为g.求:线框在竖直位置时,ab边两端的电压及所受安培力的大小;
在这一过程中,通过线框导线横截面的电荷量。