设函数f ( x ) =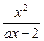 
(a ÎN*), 又存在非零自然数m, 使得f (m ) =" m" ,
f (– m ) < –
成立.
(1) 求函数f ( x )的表达式;
(2) 设{an}是各项非零的数列, 若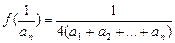
对任意nÎN*成立, 求数列{an}的一个通项公式;
在(2)的条件下, 数列{an}是否惟一确定? 请给出判断, 并予以证明.
现有编号分别为1，2，3，4，5的五个不同的语文题和编号分别为6，7，8，9，的四个不同的数学题。甲同学从这九个题中一次随机抽取两道题，每题被抽到的概率是相等的，用符号（x，y）表示事件“抽到的两题的编号分别为x、y，且
”
（1）共有多少个基本事件？并列举出来；
（2）求甲同学所抽取的两题的编号之和小于17但不小于11的概率．
在
中，
分别是角A、B、C的对边， 
，且
．
（1）求角A的大小；
（2）求
的值域．
已知函数
(
R)．
(1)当
时，求函数
的极值；
（2）若函数的图象与
轴有且只有一个交点，求的取值范围．
直线y＝kx＋b与曲线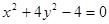
交于A、B两点，记△AOB的面积为S（O是坐标原点）．
（1）求曲线的离心率；
（2）求在k＝0，0＜b＜1的条件下，S的最大值；
（3）当｜AB｜＝2，S＝1时，求直线AB的方程．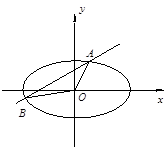
已知数列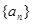
的各项均为正数，
是数列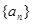的前n项和，且
．
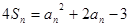（1）求数列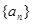的通项公式；
（2）
的值．