有一仪器中电路如图所示,其中M是质量较大的一个金属块,两端与弹簧相连接.将仪器固定在一辆汽车上.当汽车急刹车时,哪只灯亮?当汽车启动时,哪只灯亮?为什么?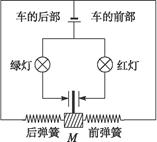
一辆汽车在十字路口等候绿灯,当绿灯亮时汽车以3 m/s2的加速度开始行驶,恰在这时一辆自行车以6 m/s的速度匀速驶来,从后边超过汽车.试求:
(1)汽车从路口开动后,在追上自行车之前经过多长时间两车相距最远?此时距离是多少?
(2)什么时候汽车追上自行车,此时汽车的速度是多少?
(1)打开水龙头,水就流下来,为什么连续的水流柱的直径在流下过程中减小?
(2)设水龙头出口直径为1 cm,安装在75 cm高处.如果水在出口处的速度为1 m/s(取g="10" m/s2),求水流柱落到地面时的直径.
建筑工人安装塔手架进行高空作业,有一名建筑工人由于不慎,抓在手中的一根长为5 m的铁杆在竖直状态下脱落了,其做自由落体运动,铁杆在下落过程中经过某一楼层面的时间为0.2 s,试求铁杆下落时其下端到该楼层的高度.(取g="10" m/s2,不计楼层面的厚度)
嫦娥一号探月卫星发射成功在政治、经济、军事、科技乃至文化领域都具有非常重大的意义。下图是嫦娥奔月过程全图。(地球半径R=6400Km,月球半径r="1700" Km)
请根据图中给出的数据
①计算出嫦娥一号卫星在距离月球200Km的圆形轨道上运行的速度。(保留3位有效数字)
②把嫦娥一号卫星工作轨道(即周期为127分钟的圆形轨道)周期 近似当作2小时,请根据图中数据计算出卫星在12小时轨道运行时,远月点与月球表面的距离。
近似当作2小时,请根据图中数据计算出卫星在12小时轨道运行时,远月点与月球表面的距离。
( ,计算结果保留2位有效数字)
,计算结果保留2位有效数字)