设函数 的定义域是R,对于任意实数
的定义域是R,对于任意实数 ,恒有
,恒有 ,且当
,且当 时,
时, .
.
(Ⅰ)求证: ,且当
,且当 时,有
时,有 ;
;
(Ⅱ)判断 在R上的单调性;
在R上的单调性;
(Ⅲ)设集合 ,集合
,集合 ,若
,若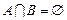 ,求
,求 的取值范围.
的取值范围.
在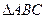 中,内角A、B、C所对的边分别为
中,内角A、B、C所对的边分别为 ,其外接圆半径为6,
,其外接圆半径为6,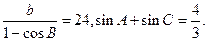
(1)求 ;
;
(2)求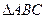 的面积的最大值。
的面积的最大值。
设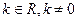 ,函数
,函数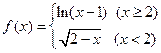 ,
,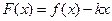 .
.
(I)试讨论函数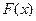 的单调性
的单调性
(II)设 ,求证:
,求证: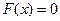 有三个不同的实根.
有三个不同的实根.
 如图,已知椭圆C:
如图,已知椭圆C: ,经过椭圆
,经过椭圆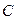 的右焦点F且斜率为
的右焦点F且斜率为 的直线l交椭圆C于A、B两点,M为线段AB的中点,设O为椭圆的中心,射线OM交椭圆于N点.
的直线l交椭圆C于A、B两点,M为线段AB的中点,设O为椭圆的中心,射线OM交椭圆于N点.
(I)是否存在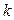 ,使对任意
,使对任意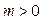 ,总有
,总有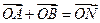 成立?若存在,求出所有
成立?若存在,求出所有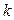 的值;
的值;
(II)若 ,求实数
,求实数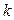 的取值范围.
的取值范围.
在数列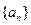 中,
中, ,
,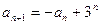 ,其中
,其中 .
.
(I)求数列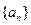 的通项公式;
的通项公式;
(II)求 的最大值.
的最大值.
某大型工厂的车床有甲,乙,丙三个型号,分别占总数的 ,
, ,
, ,现在有三名工人各自独立选一台车床操作.
,现在有三名工人各自独立选一台车床操作.
(I)求他们选择的车床类型互不相同的概率;
(II)设ξ为他们选择甲型或丙型车床的人数,求ξ的分布列及数学期望.