一根通有电流 的长直导线
的长直导线 竖直放置,另有一矩形导线框
竖直放置,另有一矩形导线框 的电流平面放在竖直平面内,通有如图所示得电流
的电流平面放在竖直平面内,通有如图所示得电流 。
。 到
到 平面得距离为
平面得距离为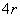 ,边长
,边长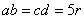 ,
, ,且
,且 和
和 两边所在处的磁感应强度大小均为
两边所在处的磁感应强度大小均为 (由
(由 产生)。求
产生)。求 和
和 所受安培力的大小,并说明方向。
所受安培力的大小,并说明方向。
据有关资料介绍,受控热核聚变反应装置中有极高的温度,因而带电粒子将没有通常意义上的容器可装,而是由磁场约束带电粒子运动将其束缚在某个区域内,现按下面的简化条件来讨论这个问题,如图所示,有一个环形区域,其截面内半径为 ,外半径为R2="1." 0 m,区域内有垂直纸面向里的匀强磁场,已知磁感应强度B="1.0" T,被束缚粒子的荷质比为
,外半径为R2="1." 0 m,区域内有垂直纸面向里的匀强磁场,已知磁感应强度B="1.0" T,被束缚粒子的荷质比为 =4.0×107C/kg,不计带电粒子在运动过程中的相互作用,不计带电粒子的重力.
=4.0×107C/kg,不计带电粒子在运动过程中的相互作用,不计带电粒子的重力.
(1)若中空区域中的带电粒子沿环的半径方向射入磁场,求带电粒子不能穿越磁场外边界的最大速度v0.
(2)若中空区域中的带电粒子以(1)中的最大速度v0沿圆环半径方向射入磁场,求带电粒子从进入磁场开始到第一次回到该点所需要的时间t。
如图所示,在某一足够大的真空室中,虚线PH的右侧是一磁感应强度为B、方向垂直纸面向里的匀强磁场,左侧是一场强为E、方向水平向左的匀强电场.在虚线PH上的点O处有一质量为M、电荷量为Q的镭核(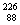 Ra).某时刻原来静止的镭核水平向右放出一个质量为m、电荷量为q的
Ra).某时刻原来静止的镭核水平向右放出一个质量为m、电荷量为q的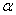 粒子而衰变为氡(Rn)核,设
粒子而衰变为氡(Rn)核,设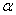 粒子与氡核分离后它们之间的作用力忽略不计,涉及动量问题时,亏损的质量可不计.
粒子与氡核分离后它们之间的作用力忽略不计,涉及动量问题时,亏损的质量可不计.
(1)写出镭核衰变为氡核的核反应方程;
(2)经过一段时间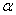 粒子刚好到达虚线PH上的A点,测得
粒子刚好到达虚线PH上的A点,测得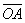 = L.求此时刻氡核的速率。
= L.求此时刻氡核的速率。
如图1-1所示,两根平行放置的金属导轨,间距为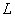 ,倾角为
,倾角为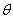 ,导轨间有电动势
,导轨间有电动势 、内阻不计的电源。现将一质量为
、内阻不计的电源。现将一质量为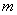 、电阻为
、电阻为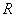 的铜棒
的铜棒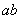 与轨道垂直放于导轨上,导轨与铜棒间的动摩擦因数为
与轨道垂直放于导轨上,导轨与铜棒间的动摩擦因数为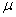 ,导轨电阻不计,要使
,导轨电阻不计,要使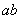 棒静止在在导轨上,所施加的竖直向上的磁场磁感应强度应多大?
棒静止在在导轨上,所施加的竖直向上的磁场磁感应强度应多大?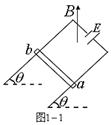
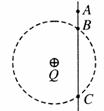
如图所示,光滑绝缘细杆竖直放置,它与以正电荷Q为圆心的某圆交于B、C两点,质量为m、带电荷量-q的有孔小球从杆上A点无初速度下滑,已知q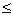 Q,AB=h,小球滑到B点时的速度大小为
Q,AB=h,小球滑到B点时的速度大小为 求:
求:
(1)小球由A到B的过程中电场力做的功;
(2)A、C两点的电势差