如图所示,两块大小不同、质量分别为M和m的圆形薄板(厚度不计),半径分别为R和r,M=3m,两板之间用一根长为L=0.4m的轻绳相连结,开始时两板水平放置并叠合在一起处在静止状态,在其正下方0.8m处有一固定支架C,支架上有一半径为R'(r<R'<R)的圆孔,圆孔与两薄板中心均在圆孔中心轴线上,今使两板一起无初速自由下落,空气阻力忽略不计.大板与支架C发生没有机械能损失的弹性碰撞,碰撞后,两块板即分离,直到轻绳绷紧,在轻绳绷紧的瞬间,两板便获得共同速度.试求这个共同速度的大小.(g取m/ )
)
图13-7-12中A、B、C为平行纸面的匀强电场中的三个点,已知B点电势为零.现将一电荷量q=10-5 C的正点电荷由A点移到C点,电场力做功W1=8×10-5 J;将该电荷由C点移到B点,电场力做功W2=-2×10-5 J.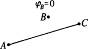
图13-7-12
(1)试求各点电势;
(2)画出场中电场线及等势面的分布情况.
如图13-7-10所示,两平行金属板相距10 cm,两板间加电压40 V,两板间有A、B、C三点,A距上板2 cm,B距下板2 cm.若把一个电荷量为3×10-4 C的负电荷沿路径ACB从A点移到B点,电场力做的功是多少?若把它从A点沿AB移到B点,电场力做的功是多少?若把它从A点沿ACBA路径又移回到A点,电场力做的功是多少? 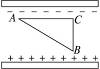
图13-7-10
如图13-7-9所示为一个匀强电场中的三个等势面A、B、C,相邻两等势面之间的距离为10 cm,此电场的场强为3×103 V·m-1,若B为零电势,求A、C的电势.
图13-7-9
如图所示,平行金属带电极板A、B间可看成匀强电场,场强E=1.2×102 V/m,极板间距离d="5" cm,电场中C和D分别到A、B两板距离均为0.5 cm,B板接地.求:
(1)C和D两点的电势、两点间电势差各为多少?
(2)将点电荷q=2×10-2 C从C匀速移到D时外力做多少功?
平行的金属板A、B间是匀强电场,如图13-7-11所示,两板间的距离是5 cm,两板间的电压是60 V.
(1)求两板间的场强;
(2)电场中有P、Q两点,P点离A板的距离为0.5 cm,Q点离B板的距离为0.5 cm,求P、Q两点之间的电势差为多少?
(3)若B板接地,P、Q两点的电势为多少?
图13-7-11