如图所示,甲、乙两小孩各乘一辆冰车在山坡前的水平冰道上游戏。甲和他的冰车总质量 =40kg,从山坡上自由下滑到水平冰道上的速度
=40kg,从山坡上自由下滑到水平冰道上的速度 =3m/s;乙和他的冰车总质量
=3m/s;乙和他的冰车总质量 =60kg,以大小为
=60kg,以大小为 =0.5m/s的速度迎着甲滑来,与甲相碰。若不计一切摩擦,小车也不直接接触,问相碰时,甲对乙施加的推力对乙做功在什么范围内,才能使两车分开,并且以后在原直线上运动甲、乙俩人不再相碰?(山坡与水平冰道连接处为圆弧形)
=0.5m/s的速度迎着甲滑来,与甲相碰。若不计一切摩擦,小车也不直接接触,问相碰时,甲对乙施加的推力对乙做功在什么范围内,才能使两车分开,并且以后在原直线上运动甲、乙俩人不再相碰?(山坡与水平冰道连接处为圆弧形)
微粒的轨迹所在平面及圆心O的位置.
(1)开关S断开和接通时,通过R1的电流分别为多大?
(2)为了使A、B之间电路的电功率在开关S接通时能达到最大值,应将R1的阻值调到多大?这时A、B间电路消耗的电功率将是多少?
在科技活动中某同学利用自制的电子秤来称量物体的质量,如图所示,为电子秤的原理图,托盘和弹簧的电阻与质量均不计.滑动变阻器的滑动端与弹簧上端连接,当托盘中没有放物体时,电压表示数为零.设变阻器的总电阻为R,总长度为l,电源电动势为E,内阻为r,限流电阻的阻值为R0,弹簧劲度系数为k,不计一切摩擦和其他阻力,电压表为理想表,当托盘上放上某物体时,电压表的示数为U,求此时称量物体的质量.
(1)t=0时刻,两只电表的示数分别是多少;
(2)在一个周期内,外力所做的功。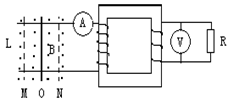
(1)请分析二极管是否发光?
(2)到了节日,要想在傍晚时天亮一点就点,应该把R1的阻值调大些还是调小些?