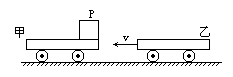
如图所示，甲车质量为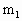
=3kg，静止在光滑的水平面上，在甲车右端放一质量为
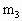=1kg的物体P(可视为质点)，另一质量为
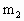=4kg的乙车以v=7m／s的速度向左运动，跟甲车发生正碰，碰后甲车以
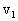=8m／s的速度向左运动，物体P滑到乙车上，P与乙车平板间的动摩擦因数
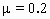，g=10
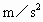，试求：
(1)P在乙车上停止时，乙车的速度是多大？
(2)P在乙车上滑行的距离是多少？
(3)在整个过程中损失的机械能是多少？
小车上固定一截面积为S的一端封闭的均匀玻璃管,管内用长为L的水银柱封住一段气体,如图所示,若大气压强为p0,则小车向左以加速度a运动时,管内气体的压强是_______(水银的密度为ρ).
如图所示,一端封闭的横截面积为S的细玻璃管中,一质量为m的活塞下面封闭有一定质量的气体.当整个系统以加速度a(a<g)加速下降时,被封闭气体的压强多大?
如图12-1-6所示，在光滑水平面上放一个质量为M、内外壁都光滑的气缸，活塞质量为m，横截面积为S，外界气压为p.现对活塞施以水平恒力F，当活塞与气缸无相对滑动时，气缸内气体压强为多大？
图12-1-6
如图12-1-5所示，U形管竖直静止放置，左端封闭，右端开口向上，用水银封闭一部分气体A，左侧水银面比右侧水银面高h，已知外界大气压为p0，水银密度为ρ，求被封气体A的压强.
图12-1-5
如图12-1-4所示，玻璃管中用h高水银柱封闭着一段气柱，求封闭气柱的压强为（设大气压强为p0，水银密度为ρ）.
图12-1-4