如图,长为L的细线一端拴一个质量为m的小球A,另一端固定在O点,A静止时恰与光滑水平桌面接触,但无相互作用力,它可以绕O点在竖直平面内做圆周运动,另一个质量也是m的金属块B以初速 在桌面上运动,并与A发生弹性正碰,求
在桌面上运动,并与A发生弹性正碰,求 至少多大,B才能从右边滑出桌面?(A、B都可看作质点)
至少多大,B才能从右边滑出桌面?(A、B都可看作质点)
1000T的列车由车站出发做匀加速直线运动,列车经过100s,通过的路程是1000m,已知运动阻力是车重的0.005倍,求列车机车的牵引力大小?
质量为10kg的物体在倾角为370的斜面底部受一个沿斜面向上的力F=100N作用,由静止开始运动。2s内物体在斜面上移动了4m,2s末撤去力F,求F撤去后,经过多长时间物体返回斜面底部(g=10m/s2)?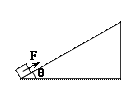
质量为12kg的箱子放在水平地面上,箱子和地面的滑动摩擦因数为0.3,现用倾角为37°的60N力拉箱子,如图所示,3s末撤去拉力,则撤去拉力时箱子的速度为多少?箱子继续运动多少时间而静止?
一个质量为2Kg的物体放在水平面上,它与水平面间的动摩擦因数μ=0.2,物体受到5N的水平拉力作用,由初速度v0=5m/s开始运动,求第4秒内物体的位移(g取10m/s2)
如图所示,在同一竖直线上有A、B两点,相距为h,B点离地高度为H,现在要在地面上寻找一点P,使得从A、B两点分别向点P安放的光滑木板,满足物体从静止开始分别由A和B沿木板下滑到P点的时间相等,求O、P两点之间的距离 。
。