一台小型发动机在3 V电压下工作,通过它的电源的电流是0.2 A,用此电动机提升重力为4 N的物体时,在30 s内可使该物体匀速提升3 m.若不计除电动机线圈发热以外的其他能量损失,求在提升重物的30 s内,电动机线圈所产生的热量.
从空中以40 m/s的初速度平抛一个质量为1 kg的物体,3 s后物体落至地面,不计空气阻力,求3 s内重力所做的功、重力的平均功率和落地时重力的瞬时功率(取g=10m/s2).
如图7-2-12所示,水平传送带以恒定的速率v="2.0" m/s运送质量m="0.5" kg的工件,工件都是在位置A处无初速地放到传送带上的,工件与传送带间的动摩擦因数μ=0.4,每当前一个工件在传送带上停止相对运动时,后一个工件即放到传送带上.求(取g="10" m/s2)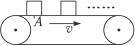
图7-2-12
(1)传送带上相邻工件间的距离;
(2)传送带克服工件的摩擦阻力做功的功率及摩擦力对工件做功的平均功率.
一辆重5 t的汽车,发动机的额定功率为80 kW.汽车从静止开始以加速度a=1 m/s2做匀加速直线运动,车受的阻力为车重的0.06倍,g取10 m/s2,求:
(1)汽车做匀加速直线运动的最长时间tm;
(2)汽车开始运动后5 s末和15 s末的瞬时功率.
火车在运行中保持额定功率2 500 kW,火车的总质量是1 000 t.所受阻力恒定为1.56×105 N.求:
(1)火车的加速度是1 m/s2时,速度是多大?
(2)火车的速度是12 m/s时,加速度是多大?
(3)火车的最大速度是多大?
额定功率为80 kW的汽车,在平直公路上行驶的最大速度是20 m/s,汽车的质量是2 t,如果汽车从静止开始做匀速直线运动,加速度的大小是2 m/s2,运动过程中所受阻力不变,试求:
(1)汽车受到的阻力多大?
(2)3 s末汽车的瞬时功率多大?
(3)汽车维持匀加速运动的时间是多少?