(18分)如图甲所示(俯视图),相距为2L的光滑平行金属导轨水平放置,导轨一部分处在以OO/为右边界匀强磁场中,匀强磁场的磁感应强度大小为B,方向垂直导轨平面向下,导轨右侧接有定值电阻R,导轨电阻忽略不计。在距边界OO/也为L处垂直导轨放置一质量为m、电阻不计的金属杆ab。求解以下问题:
(1)若ab杆固定在轨道上的初始位置,磁场的磁感应强度在时间t内由B均匀减小到零,求此过程中电阻R上产生的焦耳热为Q1。
(2)若磁场的磁感应强度不变,ab杆在恒力作用下由静止开始向右运动3L距离,其v--x的关系图像如图乙所示。求①ab杆在刚要离开磁场时的加速度大小;②此过程中电阻R上产生的焦耳热Q2 。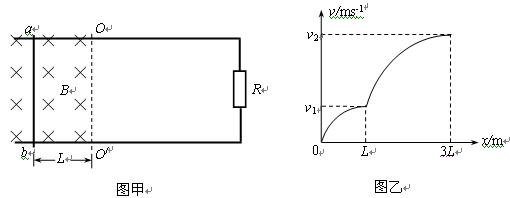
如图所示,竖直平面内的3/4圆弧形光滑轨道半径为R,A端与圆心O等高,AD为水平面,B点为光滑轨道的最高点且在O的正上方,一个小球在A点正上方由静止释放,自由下落至A点进入圆轨道并恰好能通过B点,最后落到水平面C点处。求:
(1)小球通过轨道B点的速度大小;
(2)释放点距A点的竖直高度;
(3)落点C与A点的水平距离。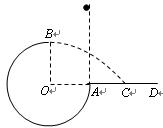
如图所示,半径分别为 、
、 的两同心虚线圆所围空间分别存在电场和磁场,中心O处固定一个半径很小(可忽略不计)的金属球,在小圆空间内存在沿半径向内的辐向电场,小圆周与金属球间电势差为
的两同心虚线圆所围空间分别存在电场和磁场,中心O处固定一个半径很小(可忽略不计)的金属球,在小圆空间内存在沿半径向内的辐向电场,小圆周与金属球间电势差为 ,两圆之间的空间存在垂
,两圆之间的空间存在垂 直于纸面向里的匀强磁场,设有一个带负电的粒子从金属球表面沿
直于纸面向里的匀强磁场,设有一个带负电的粒子从金属球表面沿 轴正方向以很小的初速度逸出,粒子质量为
轴正方向以很小的初速度逸出,粒子质量为 ,电荷量为
,电荷量为 ,(不计粒子的重力,忽略粒子逸出的初速度)求:
,(不计粒子的重力,忽略粒子逸出的初速度)求:
(1)粒子到达小圆周上时的速度为多大?
(2)粒子以(1)中的速度进入两圆间的磁场中,当磁感应强度超过某一临界值时,粒子将不能到达大圆周,求此磁感应强度的最小值 .
.
(3)若磁感应强度取(2)中最小值,且 ,要使粒子恰好第一次沿逸出方向的反方向回到原出发点,粒子需经过多少次回旋?并求粒子在磁场中运动的时间.(设粒子与金属球正碰后电量不变且能以原速率原路返回)
,要使粒子恰好第一次沿逸出方向的反方向回到原出发点,粒子需经过多少次回旋?并求粒子在磁场中运动的时间.(设粒子与金属球正碰后电量不变且能以原速率原路返回)
如图甲所示,物块A、B的质量分别是mA=" 4.0kg" 和mB= 3.0kg,用轻弹簧栓接相连放在光滑的水平地面上,物块B右侧与竖直墙相接触.另有一物块C从t =0时以一定速度向右运动,在t =" 4" s 时与物块A相碰,并立即与A粘在一起不再分开.物块C的v-t 图象如图乙所示.求:
(1)物块C的质量mC;
(2)墙壁对物块B的弹力在4 s 到12 s 的时间内对B做的功W及对B的冲量I的大小和方向;
(3)B离开墙后的过程中弹簧具有的最大弹性势能EP.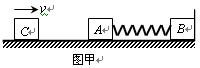
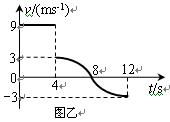
一个物块放置在粗糙的水平地面上,受到的水平拉力F随时间t变化的关系如图(a)所示,速度v随时间t变化的关系如图(b)所示(g=10m/s2).求:
(1)1s末物块所受摩擦力的大小f1;
(2)物块在前6s内的位移大小 ;
;
(3)物块与水平地面间的动摩擦因数μ.
