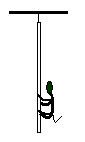

一质量为M的直木棒,悬挂在O点。一只质量为m的猴子抓住木棒,如图所示。剪断悬挂木棒的细绳,木棒开始下落,同时猴子开始沿木棒向上爬。设一段时间内木棒的下落是沿竖直方向,并且猴子对地的高度保持不变。忽略空气阻力。则图所示的4个图象中哪个能定性地反映在这段时间内猴子做功的功率随时间变化的关系?
质点做直线运动的位移x与时间t的关系为x = 4t+t2(各物理量均采用国际单位制单位),则该质点第3秒末的速度比第2秒初的速度大m/s,第2秒内的位移m 。
如图所示,a、b分别是甲、乙两辆车从同一地点沿同一直线同时运动的速度图象,由图象可以判断( )
| A.2 s后甲、乙两车的加速度大小相等 |
| B.在0~8 s内两车最远相距148 m |
| C.两车只有t0时刻速率相等 |
| D.两车在t=8 s时相遇 |
一辆公共汽车进站后开始刹车,做匀减速直线运动,开始刹车后的第1 s内和第3 s内位移大小依次为9 m和5 m,则刹车后6 s内的位移是()
| A.20 m | B.24 m | C.25 m | D.75 m |
甲、乙两车在公路上沿同一方向做直线运动,它们的 v-t图象如图所示。两图象在t=t1时相交于P点,P在横轴上的投影为Q,△OPQ的面积为S。在t=0时刻,乙车在甲车前面,相距为d。已知此后两车相遇两次,且第一次相遇的时刻为t′,则下面四组t′和d的组合可能的是()
A. |
B. |
C. |
D. |
物体做匀加速直线运动,在时间T内通过位移x1到达A点,接着在时间T内又通过位移x2到达B点,则物体()
A.在A点的速度大小为  |
B.在B点的速度大小为  |
C.运动的加速度为 |
D.运动的加速度为 |