已知A、B、C为三个锐角,且A+B+C=π.若向量=(2-2sinA,cosA+sinA)与向量=(cosA-sinA,1+sinA)是共线向量.(Ⅰ)求角A;(Ⅱ)求函数y=2sin2B+cos的最大值.
已知函数
,其中
.
(1)设
是
的导函数,评论
的单调性;
(2)证明:存在
,使得
在区间
内恒成立,且
在
内有唯一解.
如图,椭圆
的离心率是
,过点
的动直线
与椭圆相交于
两点,当直线
平行与
轴时,直线
被椭圆
截得的线段长为
.

(1)求椭圆
的方程;
(2)在平面直角坐标系
中,是否存在与点
不同的定点
,使得
恒成立?若存在,求出点
的坐标;若不存在,请说明理由.
如图,
为平面四边形
的四个内角.

(1)证明: ,
(2)若 求 的值.
一个正方体的平面展开图及该正方体的直观图的示意图如图所示,在正方体中,设 的中点为 , 的中点为
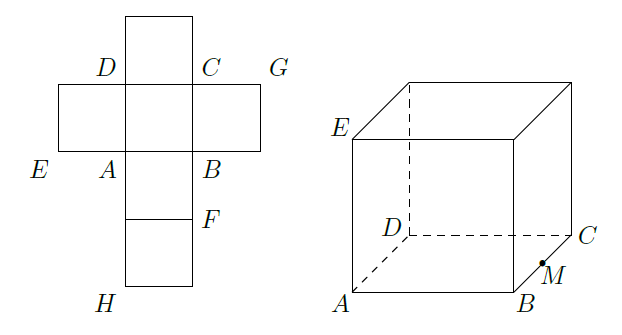
(1)请将字母
标记在正方体相应的顶点处(不需说明理由)
(2)证明:直线
平面
(3)求二面角 的余弦值
某市
两所中学的学生组队参加辩论赛,
中学推荐3名男生,2名女生,
中学推荐了3名男生,4名女生,两校推荐的学生一起参加集训,由于集训后队员的水平相当,从参加集训的男生中随机抽取3人,女生中随机抽取3人组成代表队
(1)求
中学至少有1名学生入选代表队的概率.
(2)某场比赛前,从代表队的6名队员中随机抽取4人参赛,设
表示参赛的男生人数,求
得分布列和数学期望.