学校文娱队的每位队员唱歌、跳舞至少会一项,已知会唱歌的有2人,会跳舞的有5人,现从中选2人.设ξ为选出的人中既会唱歌又会跳舞的人数,且P(ξ>0)=.(Ⅰ)求文娱队的人数;(Ⅱ)写出ξ的概率分布列并计算Eξ.
已知数列 的前
的前 项和
项和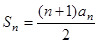 ,且
,且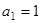 。
。
(1)求数列 的通项公式;
的通项公式;
(2)令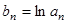 ,是否存在
,是否存在 (
(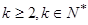 ),使得
),使得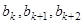 成等比数列。若存在,求出所有符合条件的
成等比数列。若存在,求出所有符合条件的 值;若不存在,请说明理由。
值;若不存在,请说明理由。
已知函数 成等差数列, 点
成等差数列, 点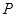 是函数
是函数 图像上任意一点,点
图像上任意一点,点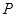 关于原点的对称点
关于原点的对称点 的轨迹是函数
的轨迹是函数 的图像
的图像
(1)解关于 的不等式
的不等式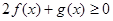 ;
;
(2)当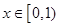 时,总有
时,总有 恒成立,求
恒成立,求 的取值范围.
的取值范围.
已知二次函数 的二次项系数为
的二次项系数为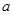 ,且不等式
,且不等式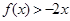 的解集为
的解集为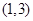 ,
,
(1)若方程 有两个相等的实根,求
有两个相等的实根,求 的解析式;
的解析式;
(2)若 的最大值为正数,求
的最大值为正数,求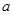 的取值范围.
的取值范围.
设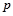 :实数
:实数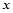 满足
满足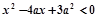 ,其中
,其中 ,
, :实数
:实数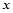 满足
满足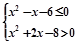 .
.
(1)若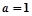 且
且 为真,求实数
为真,求实数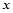 的取值范围;
的取值范围;
(2)若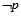 是
是 的充分不必要条件,求实数
的充分不必要条件,求实数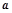 的取值范围.
的取值范围.
在△ABC中,角A,B,C的对边分别是a,b,c,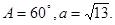 ,
,
(1)若 ,求
,求 的值.
的值.
(2)若△ABC是锐角三角形时,求 的取值范围。
的取值范围。