地球表面的重力加速度为g=10m/s2,地球半径R=6.4×106m,万有引力常量G=6.67×10-11N.m2/kg2,假设地球是一个质量分布均匀的球体,则地球的平均密度(单位:kg/m3,保留一位有效数字)是:( )
| A.6×102 | B.1×103 | C.6×103 | D.6×104 |
在均匀介质中选取平衡位置在同一直线上的9个质点,相邻两质点间的距离均为L,如图a所示。一列简谐横波沿该直线向右传播,t=0时到达质点1处,质点1开始向下运动,经过时间D t第一次出现如图b所示波形。则该波的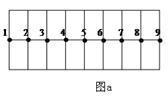

A.周期为 ,波长为8L ,波长为8L |
B.周期为 ,波长为8L ,波长为8L |
C.周期为 ,波速为 ,波速为 |
D.周期为 ,波速为 ,波速为 |
如图所示,绝热的汽缸与绝热的活塞A、B密封一定质量的空气后水平放置在光滑地面上,不计活塞与汽缸壁的摩擦,现用电热丝给汽缸内的气体加热,在加热过程中
A.汽缸向左移动
B.活塞A、B均向左移动
C.密封气体的内能一定增加
D.汽缸中单位时间内作用在活塞A和活塞B的分子个数相同
如图所示,ABCD为同种材料构成的柱形透明体的横截面,其中ABD部分为等腰直角三角形,BCD部分为半圆形,一束单色平行光从真空垂直射向AB或AD面,材料的折射率n=1.6,下列说法中正确的是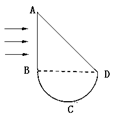
| A.从AB面中点射入的光线不一定从圆弧的中点射出 |
| B.从AB面射入的所有光线经一次反射和折射后都能从BCD面射出 |
| C.从AB面中间附近射入的光线经一次反射和折射后能从BCD面射出 |
| D.若光线只从AD面垂直射入,则一定没有光线从BCD面射出 |
1964年至1967年6月我国第一颗原子弹和第一颗氢弹相继试验成功,1999年9月18日,中共中央、国务院、中央军委隆重表彰在研制“两弹一星”中作出贡献的科学家。下列核反应方程式中属于原子弹爆炸的核反应方程式的是
A. U→ U→ Th + Th + He He |
B. U + U + n→ n→ Sr + Sr + Xe +10 Xe +10 n n |
C. N + N + He→ He→ O + O + H H |
D. H + H + H→ H→ He + He + n n |
下列说法正确的是
| A.气体能充满任何容器是因为分子间的排斥力大于吸引力 |
| B.可以将流散到周围环境中的内能重新收集起来加以利用而不引起其他变化 |
| C.测出油酸分子的大小,并已知油酸的摩尔体积,就可以估算出阿伏伽德罗常数 |
| D.一定质量的气体,温度升高时,压强一定变大 |