如图所示,在直角坐标系的第一、四象限内有垂直于纸面的匀强磁场,第二、三象限内有沿x轴正方向的匀强电场,电场强度大小为E,y轴为磁场和电场的理想边界. 一个质量为m,电荷量为e的质子经过x轴上A点时速度大小为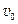 ,速度方向与x轴负方向夹角θ=30º. 质子第一次到达y轴时速度方向与y轴垂直,第三次到达y轴的位置用B点表示,图中未画出,已知OA=l,不计质子重力影响.
,速度方向与x轴负方向夹角θ=30º. 质子第一次到达y轴时速度方向与y轴垂直,第三次到达y轴的位置用B点表示,图中未画出,已知OA=l,不计质子重力影响.
(1)求磁感应强度的大小和方向;
(2)求质子从A点运动至B点时间. 
如图8-3-9所示,粗细均匀,两端开口的U形管竖直放置,管的内径很小,水平部分BC长14 cm.一空气柱将管内水银分离成左右两段.大气压强相当于高为76 cmHg的压强.
图8-3-9
(1)当空气柱温度为T0="273" K,长为l0="8" cm时,BC管内左边水银柱长2 cm,AB的管内水银柱长是2 cm,则右边水银柱总长是多少?
(2)当空气柱温度升高到多少时,左边的水银恰好全部进入竖直管AB内?
(3)当空气柱温度为490 K时,两竖直管内水银柱上表面高度各为多少?
如图8-3-12所示,一个密闭的气缸,被活塞分成体积相等的左、右两室,气缸壁与活塞是不导热的;它们之间没有摩擦,两室中气体的温度相等,现利用右室中的电热丝对右室加热一段时间,达到平衡后,左室的体积变为原来的 ,气体的温度T1="300" K,求右室气体的温度.
,气体的温度T1="300" K,求右室气体的温度.
图8-3-12
如图10-4-1所示,一定质量理想气体由状态A经过程Ⅰ变至状态B时,从外界吸收热量420 J,同时膨胀对外做功300 J.当气体从状态B经过Ⅱ回到状态A时,外界压缩气体做功200 J.求此过程中气体是吸热还是放热,热量是多少.
图10-4-1
用火箭把质量m=1.0×103 kg的卫星发射到接近地面的圆形轨道上绕地球运行.已知地球半径R=6.4×106 m,火箭内所装燃料的热值q=6.4×107 J/kg,地面附近的重力加速度g="9.8" m/s2.若燃料完全燃烧产生的热量有1%转化为卫星运行时的动能,火箭内所装燃料的质量至少为多少?
如图7-2-16所示,U=10V,电阻R1=3Ω,R2=2Ω,R3=5Ω,电容器的电容C1=4μF,C2=1μF,求: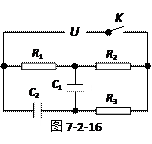
(1)当K闭合时间足够长时,C1和C2所带的电量各是多少?
(2)然后把K断开,K断开后通过R2的电量是多少?