已知函数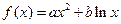 在
在 处有极值
处有极值 .
.
(Ⅰ)求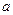 ,
,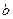 的值;
的值;
(Ⅱ)判断函数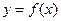 的单调性并求出单调区间.
的单调性并求出单调区间.
某纺纱厂生产甲、乙两种棉纱,已知生产甲种棉纱1吨需耗一级籽棉2吨、二级籽棉1吨;生产乙种棉纱1吨需耗一级籽棉1吨,二级籽棉2吨.每1吨甲种棉纱的利润为900元,每1吨乙种棉纱的利润为600元.工厂在生产这两种棉纱的计划中,要求消耗一级籽棉不超过250吨,二级籽棉不超过300吨.问甲、乙两种棉纱应各生产多少吨,能使利润总额最大?并求出利润总额的最大值.
如图,在四边形ABCD中,AC平分∠DAB,∠ABC=60°,AC=6,AD=5,S△ADC=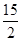 ,求AB的长.
,求AB的长.
设等差数列{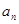 }的前
}的前 项和为
项和为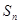 ,已知
,已知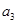 =
= ,
,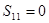 .
.
(Ⅰ) 求数列{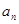 }的通项公式;
}的通项公式;
(Ⅱ)求数列{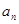 }的前n项和
}的前n项和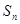 ;
;
(Ⅲ)当n为何值时,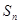 最大,并求
最大,并求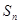 的最大值.
的最大值.
已知函数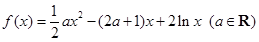 .
.
(1)若曲线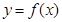 在
在 和
和 处的切线互相平行,求
处的切线互相平行,求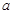 的值;
的值;
(2)求 的单调区间;
的单调区间;
(3)设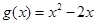 ,若对任意
,若对任意 ,均存在
,均存在 ,使得
,使得 ,求
,求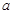 的取值范围.
的取值范围.
如图,在平面直角坐标系 中,设点
中,设点 (
(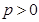 ),直线
),直线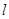 :
: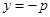 ,点
,点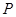 在直线
在直线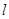 上移动,
上移动, 是线段
是线段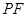 与
与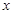 轴的交点, 过
轴的交点, 过 、
、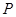 分别作直线
分别作直线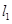 、
、 ,使
,使 ,
,
 .
.
(1)求动点 的轨迹
的轨迹 的方程;
的方程;
(2)在直线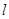 上任取一点
上任取一点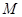 做曲线
做曲线 的两条切线,设切点为
的两条切线,设切点为 、
、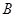 ,求证:直线
,求证:直线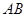 恒过一定点;
恒过一定点;
(3)对(2)求证:当直线 的斜率存在时,直线
的斜率存在时,直线 的斜率的倒数成等差数列.
的斜率的倒数成等差数列.