某学生在上学路上要经过4个路口，假设在各路口是否遇到红灯是相互独立的，遇到红灯的概率都是
，遇到红灯时停留的时间都是2min.
（1）求这名学生在上学路上到第三个路口时首次遇到红灯的概率；
（2）求这名学生在上学路上因遇到红灯停留的总时间至多是4min的概率.
本小题满分14分
正方形
的边长为1，分别取边
的中点
，连结
，
以为折痕，折叠这个正方形，使点
重合于一点
，得到一
个四面体，如下图所示。
 |
（1）求证：
；
（2）求证：平面
。
.(本题14分)
如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧棱PD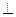
底面ABCD，PD=DC，
E是PC的中点，作EF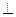PB交PB于点F。
（1）证明：PA//平面EDB；
（2）证明：PB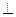平面EFD。
 |
一个几何体的三视图如图所示（单位长度为：cm）：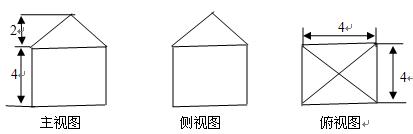
主视图侧视图俯视图
（1）求该几何体的体积；
（2）求该几何题的表面积。
（本题12分）
求满足下列条件的直线方程：
（1）过点（2，3），斜率是直线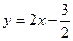
斜率的一半；
（2）过点（1，0），且过直线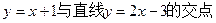
（本题12分）
已知直线
（1）若
平行，求
的值。
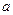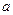（2）若垂直，求的值。