如图，已知正三棱柱
—
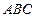的底面边长是
，
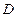是侧棱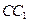
的中点，直线
与侧面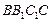
所成的角为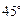
．
（Ⅰ）求此正三棱柱的侧棱长；
（Ⅱ）求二面角
的大小；
（Ⅲ）求点
到平面
的距离．
在一个盒子中有
个球，其中2个球的标号是不同的偶数，其余n个球的标号是不同的奇数。甲乙两人同时从盒子中各取出2个球，若这4个球的标号之和为奇数，则甲胜；若这4个球的标号之和为偶数，则乙胜。规定：胜者得2分，负者得0分。
（I）当
时，求甲的得分
的分布列和期望；
（II）当乙胜概率为
的值
在△ABC中，角A，B，C所对的边分别为a，b，c，且满足
（I）求角B的大小；
（II）若b是a和c的等比中项，求△ABC的面积
（本小题满分13分）设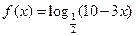
．（1）求使
≥1的x的取值范围；（2）若对于区间 [2，3]上的
每一个x的值，不等式＞
恒成立，求实数m的取值范围．
（（本小题满分14分）如图，正方体
中，棱长为
（1）求直线
与
所成的角；
（２）求直线
与平面
所成角的正切值；
（３）求证：平面
平面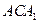
．
（本小题满分12分）
已知AD是Rt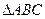
斜边BC的中线，用解析法证明
．