函数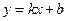 ,其中
,其中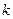 、
、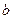
 是常数,其图象是一条直线,称这个函数为线性函数.对于非线性可导函数
是常数,其图象是一条直线,称这个函数为线性函数.对于非线性可导函数 ,在点
,在点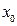 附近一点
附近一点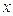 的函数值
的函数值 ,可以用如下方法求其近似代替值:
,可以用如下方法求其近似代替值: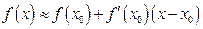 .利用这一方法,
.利用这一方法, 的近似代替值
的近似代替值
A.大于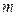 |
B.小于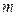 |
C.等于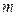 |
D.与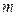 的大小关系无法确定 的大小关系无法确定 |
某调查机构对本市小学生课业负担情况进行了调查,设平均每
人每天做作业的时间为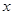 分钟.有1000名小学生参加了此项调
分钟.有1000名小学生参加了此项调
查,调查所得数据用程序框图处理,若输出的结果是680,则
平均每天做作业的时间在0~60分钟内的学生的频率是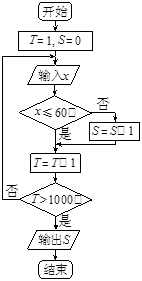
| A. 680 | B. 320 |
| C. 0.68 | D. 0.32 |
.已知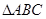 的三个内角A、B、C所对的边分别为
的三个内角A、B、C所对的边分别为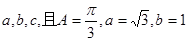 ,则角B等于
,则角B等于
A.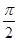 B.
B.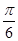 C.
C.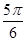 D.
D.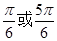
右图是某四棱锥的三视图,则该几何体的表面积等于 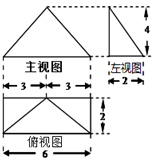
A.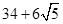 |
B. |
C.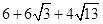 |
D.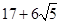 |
设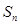 为等比数列
为等比数列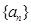 的前
的前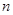 项和,
项和,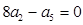 ,则
,则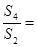
A.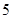 |
B.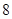 |
C.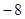 |
D.15 |
已知命题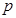 :抛物线
:抛物线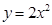 的准线方程为
的准线方程为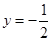 ;命题
;命题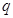 :若函数
:若函数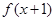 为偶函数,则
为偶函数,则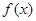 关于
关于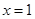 对称.则下列命题是真命题的是
对称.则下列命题是真命题的是
A.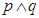 |
B.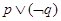 |
C.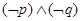 |
D.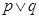 |