已知等差数列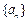
的首项为a，公差为b，等比数列
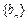的首项为b，公比为a，其中a，b都是大于1的正整数，且
．
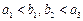（1）求a的值；
（2）若对于任意的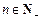
，总存在
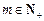，使得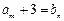
成立，求b的值；
（3）令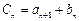
，问数列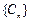
中是否存在连续三项成等比数列？若存在，求出所有成等比数列的连续三项；若不存在，请说明理由．
已知等差数列
是递增数列，且满足
（1）求数列的通项公式；
（2）令
，求数列
的前
项和
如图，在四棱锥
中，底面
是矩形，侧棱PD⊥底面ABCD，PD＝DC，E是PC的中点，作EF⊥PB交PB于点F.
（1）证明：PA∥平面EDB；
（2）证明：PB⊥平面EFD.
已知成等差数列的三个正数的和为15，并且这三个数分别加上2、5、13后成为等比数列
中的
(1) 求数列的通项公式；
(2) 数列的前n项和为
，求证：数列
是等比数列.
已知函数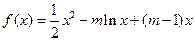 
，
．
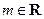(Ⅰ）当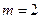 
时，求函数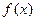 
的最小值；
(Ⅱ）当 
时，讨论函数 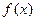的单调性；
(Ⅲ）求证：当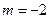 
时，对任意的 
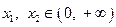，且
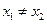，有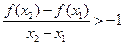
．
如下图，互相垂直的两条公路
、
旁有一矩形花园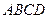
，现欲将其扩建成一个更大的三角形花园
，要求点
在射线上，点
在射线上，且直线
过点
，其中
米，
米. 记三角形花园的面积为
.
(Ⅰ）当
为何值时，取得最小值，并求出最小值；
(Ⅱ）若不超过1764平方米，求长的取值范围.