若A={x|x2-2x-3<0},B={x|(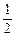 )x-a
)x-a 1}
1}
(1)当A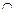 B=
B=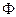 时,求实数a的取值范围;
时,求实数a的取值范围;
(2) 当A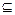 B时,求实数a的取值范围
B时,求实数a的取值范围
如图1,在△ABC中,BC=3,AC=6,∠C=90°,且DE∥BC,将△ADE沿DE折起到△A1DE的位置,使A1D⊥CD,如图2。
(1)求证:BC⊥平面A1DC;
(2)若CD=2,求BE与平面A1BC所成角的正弦值。
已知数列 的前
的前 项和为
项和为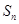 ,
,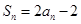 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设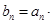 log2an+1 ,求数列
log2an+1 ,求数列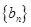 的前
的前 项和
项和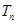 。
。
在平面直角坐标系中,若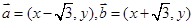 ,且
,且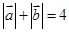 .
.
(1)求动点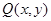 的轨迹
的轨迹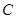 的方程;
的方程;
(2)已知定点 ,若斜率为
,若斜率为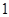 的直线
的直线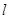 过点
过点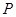 并与轨迹
并与轨迹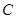 交于不同的两点
交于不同的两点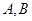 ,且对于轨迹
,且对于轨迹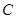 上任意一点
上任意一点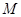 ,都存在
,都存在 ,使得
,使得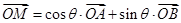 成立,试求出满足条件的实数
成立,试求出满足条件的实数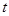 的值.
的值.
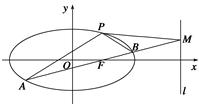
如图,椭圆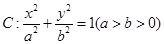 经过点
经过点 ,离心率
,离心率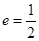 ,直线
,直线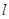 的方程为
的方程为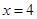 .
.
(1)求椭圆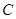 的方程;
的方程;
(2)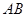 是经过右焦点
是经过右焦点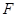 的任一弦(不经过点
的任一弦(不经过点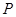 ),设直线
),设直线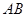 与直线
与直线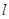 相交于点
相交于点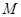 ,记
,记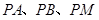 的斜率分别为
的斜率分别为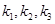 .问:是否存在常数
.问:是否存在常数 ,使得
,使得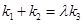 ?若存在,求
?若存在,求 的值;若不存在,说明理由.
的值;若不存在,说明理由.
已知中心在原点的双曲线 的右焦点为
的右焦点为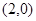 ,实轴长
,实轴长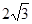 .
.
(1)求双曲线的方程
(2)若直线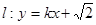 与双曲线恒有两个不同的交点
与双曲线恒有两个不同的交点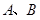 ,且
,且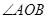 为锐角(其中
为锐角(其中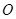 为原点),求
为原点),求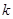 的取值范围.
的取值范围.