如图,已知:在菱形ABCD中,∠DAB=60°,PA⊥底面ABCD,PA=AB=2,E,F分别是AB与PD的中点.
(1)求证:PC⊥BD;
(2)求证:AF//平面PEC;
(3)求二面角P—EC—D的大小.
(本小题满分12分)如图,曲线 由上半椭圆
由上半椭圆 和部分抛物线
和部分抛物线
 连接而成,
连接而成, 的公共点为
的公共点为 ,其中
,其中 的离心率为
的离心率为 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)过点 的直线
的直线 与
与 分别交于
分别交于 (均异于点
(均异于点 ),若
),若 ,求直线
,求直线 的方程.
的方程.
(本小题满分12分)如图,三棱柱 中,
中, ,
, ,平面
,平面 平面
平面 ,
, 与
与 相交于点
相交于点 .
.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求二面角 的余弦值.
的余弦值.
(本小题满分12分)一个盒子中装有大量形状大小一样但重量不尽相同的小球,从中随机抽取 个作为样本,称出它们的重量(单位:克),重量分组区间为
个作为样本,称出它们的重量(单位:克),重量分组区间为 ,
, ,
, ,
, ,由此得到样本的重量频率分布直方图(如图),
,由此得到样本的重量频率分布直方图(如图),
(Ⅰ)求 的值,并根据样本数据,试估计盒子中小球重量的众数与平均值;
的值,并根据样本数据,试估计盒子中小球重量的众数与平均值;
(Ⅱ)从盒子中随机抽取 个小球,其中重量在
个小球,其中重量在 内的小球个数为
内的小球个数为 ,求
,求 的分布列和数学期望. (以直方图中的频率作为概率).
的分布列和数学期望. (以直方图中的频率作为概率).
(本小题满分12分)已知 为等差数列,且满足
为等差数列,且满足 ,
, .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)记 的前
的前 项和为
项和为 ,若
,若 成等比数列,求正整数
成等比数列,求正整数 的值.
的值.
已知函数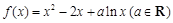 .
.
(Ⅰ)当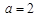 时,求函数
时,求函数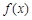 在
在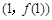 处的切线方程;
处的切线方程;
(Ⅱ)求函数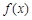 的单调区间;
的单调区间;
(Ⅲ)若函数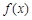 有两个极值点
有两个极值点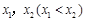 ,不等式
,不等式 恒成立,求实数
恒成立,求实数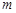 的取值范围.
的取值范围.