对任意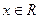 ,给定区间
,给定区间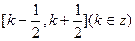 ,设函数
,设函数 表示实数
表示实数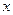 与
与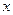 的给定区间内整数之差的绝对值.
的给定区间内整数之差的绝对值.
|
(1)当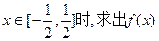 的解析式;当
的解析式;当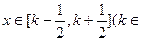 Z)时,写出用绝对值符号表示的
Z)时,写出用绝对值符号表示的 的解析式,并说明理由;
的解析式,并说明理由;

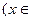 R)的奇偶性,并证明你的结论;
R)的奇偶性,并证明你的结论;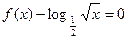 的实根.(要求说明理由)
的实根.(要求说明理由)在△ABC中,角A,B,C的对边分别为a,b,c,向量 =(cosC,sin
=(cosC,sin ),向量
),向量 =(sin
=(sin ,cosC),且
,cosC),且 .
.
(1)求角C的大小;
(2)若a2=2b2+c2,求tanA的值.
在平面直角坐标系xOy中,已知向量 =(2,0),
=(2,0), =(0,1).设向量
=(0,1).设向量 ,
,
 ,其中0<θ<
,其中0<θ< .
.
(1)若 ∥
∥ ,且θ=
,且θ= ,求实数k的值;
,求实数k的值;
(2)若 ⊥
⊥ ,求实数k的最大值,并求取最大值时cosθ的值.
,求实数k的最大值,并求取最大值时cosθ的值.
设函数 x.
x.
(1)求f(x)的单调增区间;
(2)若x∈(0,4),求y=f(x)的值域.
已知f(x)=|2x﹣1|﹣|x+1|.
(Ⅰ)求f(x)>x解集;
(Ⅱ)若a+b=1,对∀a,b∈(0,+∞), +
+ ≥|2x﹣1|﹣|x+1|恒成立,求x的取值范围.
≥|2x﹣1|﹣|x+1|恒成立,求x的取值范围.
已知在直角坐标系xOy中,直线l的参数方程为 ,(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ2﹣4ρcosθ+3=0.
,(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ2﹣4ρcosθ+3=0.
(Ⅰ)求直线l的普通方程和曲线C的直角坐标方程;
(Ⅱ)设点P是曲线C上的一个动点,求它到直线l的距离d的取值范围.