设函数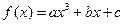
 为奇函数,其图象在点
为奇函数,其图象在点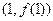 处的切线与直线
处的切线与直线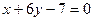 垂直,且在x=-1处取得极值.
垂直,且在x=-1处取得极值.
(Ⅰ)求a,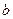 ,
,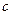 的值;
的值;
(Ⅱ)求函数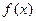 在
在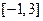 上的最大值和最小值。
上的最大值和最小值。
如图,在四棱锥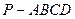 中,底面
中,底面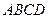 是矩形,
是矩形,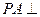 平面
平面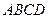 ,且
,且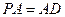 ,点
,点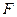 是棱
是棱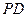 的中点,点
的中点,点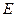 在棱
在棱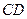 上移动.
上移动.
(Ⅰ)当点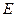 为
为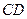 的中点时,试判断直线
的中点时,试判断直线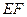 与平面
与平面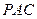 的关系,并说明理由;
的关系,并说明理由;
(Ⅱ)求证: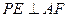 .
.
设集合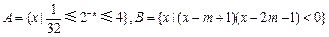 .
.
(Ⅰ)求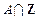 ;
;
(Ⅱ)若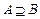 ,求
,求 的取值范围.
的取值范围.
已知函数
(I)求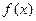 的最小正周期与单调递减区间;
的最小正周期与单调递减区间;
(II)在△ABC中,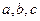 分别是角A、B、C的对边,若
分别是角A、B、C的对边,若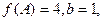 △ABC的面积为
△ABC的面积为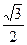 ,求
,求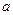 的值
的值
设二次函数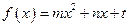 的图像过原
的图像过原 点,
点,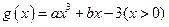 ,
,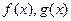 的导函数为
的导函数为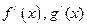 ,且
,且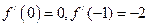 ,
,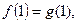
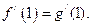
(1)求函数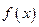 ,
, 的解析式;
的解析式;
(2)求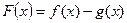 的极小值;
的极小值;
(3)是否存在实常数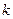
 和
和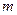 ,使得
,使得 和
和 若存在,求
若存在,求 出
出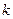 和
和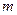 的值;若不存在,说明理由
的值;若不存在,说明理由 。
。
已知函数 的定义域为
的定义域为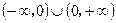 ,且满足条件:①
,且满足条件:①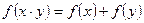 ,②
,②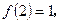 ③当
③当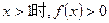 .
.
(1)求证:函数 为偶函数;
为偶函数;
(2)讨论函数 的单调性;
的单调性;
(3)求不等式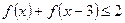 的解集
的解集