已知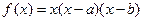 ,点
,点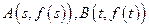 .
.
(Ⅰ)若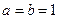 ,求函数
,求函数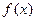 的单调递增区间;
的单调递增区间;
(Ⅱ)若函数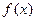 的导函数
的导函数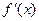 满足:当
满足:当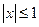 时,有
时,有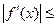
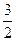 恒成立,求函数
恒成立,求函数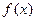 的解析表达式;
的解析表达式;
(Ⅲ)若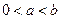 ,函数
,函数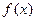 在
在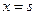 和
和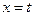 处取得极值,且
处取得极值,且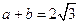 ,证明:
,证明: 与
与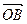 不可能垂直。
不可能垂直。
(本小题满分10分).
(1)化简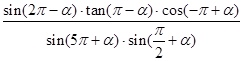
(2)求函数 的最大值及对应的
的最大值及对应的 值.
值.
下列各项中,值等于 的是
的是
A. |
B. |
C. |
D. |
已知等差数列{an}的首项a1=1,公差d>0,且第二项、第五项、第十四项分别是一个等比数列的第二项、第三项、第四项.
(1)求数列{an}的通项公式;
(2)设bn= (n∈N*),Sn=b1+b2+…+bn,是否存在最大的整数t,使得对任意的n均有Sn>
(n∈N*),Sn=b1+b2+…+bn,是否存在最大的整数t,使得对任意的n均有Sn> 总成立?若存在,求出t;若不存在,请说明理由.
总成立?若存在,求出t;若不存在,请说明理由.
在△ABC中,内角A,B,C所对的边分别为a,b,c,且a+b+c=8.
(1)若a=2,b= ,求cos C的值;
,求cos C的值;
(2)若sin Acos2 +sin Bcos2
+sin Bcos2 =2sin C,且△ABC的面积S=
=2sin C,且△ABC的面积S= sin C,求a和b的值.
sin C,求a和b的值.
数列{an}满足a1=1,a2=2,an+2=2an+1-an+2.
(1)设bn=an+1-an,证明{bn}是等差数列;
(2)求{an}的通项公式.