如图所示，在光滑水平面上有一条柔软的质量为m、长为L的均匀链条，开始时，这个链条有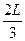
长在桌面上，而
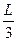长垂于桌外．若不计能量损失，求：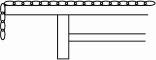
（1）把它的悬垂部分拉回到桌面，至少做多少功？
（2）如果让它由静止开始下滑，当全部链条离开桌面时，这条链条的速率是多大？
（1）E0与E1的大小；
（2）若从M点射出的粒子恰从中点S孔垂直射入边长为a的正方形容器中，容器中存在如 图所示的匀强磁场，已知粒子运动的半径小于a。欲使粒子与器壁多次垂直碰撞后仍能从S孔射出（粒子与绝缘壁碰撞时无能量和电量损失），求磁感应强度B应满足的条件？
（3）在PQ间还有许多水平射入电场的粒子通过电场后也能从CD边水平射出，这些入射点到P点的距离应满足的条件？
甲火车以4m/s的速度匀速前进，当时乙火车误入同一轨道,且以20m/s的速度追向甲车，当乙车司机发现甲车相距125m，乙车立即刹车，已知以这种速度前进的火车刹车后经过200m才能停止，问是否会发生撞车事故？
一个物体做自由落体运动，着地时的速度是经过空中P点时速度的2倍．已知P点离地面的高度h=15m，则物体着地的速度为多少？物体在空中运动的时间为多少?物体下落的总高度为多少？(不计空气阻力，g取10m/s2)