设是已知平面上所有向量的集合,对于映射,记的象为.若映射满足:对所有、及任意实数都有,则称为平面上的线性变换。现有下列命题:
①设是平面上的线性变换,、,则
②若是平面上的单位向量,对,设,则是平面上的线性变换;
③对,设,则是平面上的线性变换;
④设是平面上的线性变换,,则对任意实数均有.
其中的真命题是(写出所有真命题的编号)
(本小题满分13分)已知椭圆 的右焦点
的右焦点 与抛物线
与抛物线 的焦点重合,直线
的焦点重合,直线 :
: 与直线
与直线 :
: 之间的距离为6
之间的距离为6
(Ⅰ)求椭圆 方程;
方程;
(Ⅱ)设椭圆 的左焦点为
的左焦点为 ,
, 与
与 轴的交点为
轴的交点为 ,过点
,过点 作斜率不为零的直线与椭圆
作斜率不为零的直线与椭圆 交于
交于 两点,
两点, 关于
关于 轴对称的点为
轴对称的点为 .
.
(ⅰ)证明: 三点共线;
三点共线;
(ⅱ)求 的面积
的面积 的最大值.
的最大值.
函数 ,给出以下命题:
,给出以下命题:
①函数 有
有 个零点;
个零点;
②若 时,函数
时,函数 恒成立,则实数
恒成立,则实数 的取值范围是
的取值范围是 ;
;
③函数 的极大值中一定存在最小值;
的极大值中一定存在最小值;
④
 ,对一切
,对一切 恒成立;
恒成立;
⑤任取 ,
, ,都有
,都有 恒成立.
恒成立.
其中真命题的有
双曲线 的两个焦点为
的两个焦点为 ,若
,若 是双曲线上一点,且
是双曲线上一点,且 ,则双曲线离心率的取值范围为 .
,则双曲线离心率的取值范围为 .
三棱锥 中,
中, 平面
平面 ,
, ,则该三棱锥外接球的体积为 .
,则该三棱锥外接球的体积为 .
在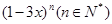 的展开式中,各项系数和为___________.
的展开式中,各项系数和为___________.