(本小题满分13分)某单位有三辆汽车参加某种事故保险,单位年初向保险公司
缴纳每辆900元的保险金.对在一年内发生此种事故的每辆汽车,单位获9000元
的赔偿(假设每辆车最多只赔偿一次)。设这三辆车在一年内发生此种事故的概率
分别为 且各车是否发生事故相互独立,求一年内该单位在此保险中:
且各车是否发生事故相互独立,求一年内该单位在此保险中:
(1)获赔的概率;(4分)
(2)获赔金额 的分别列与期望。(9分)
的分别列与期望。(9分)
已知幂函数f(x)=x (m∈Z)为偶函数,且在区间(0,+∞)上是单调减函数.
(m∈Z)为偶函数,且在区间(0,+∞)上是单调减函数.
(1)求函数f(x);
(2)讨论F(x)=a 的奇偶性.
的奇偶性.
已知函数f(x)=loga (a>0,且a≠1,b>0).
(a>0,且a≠1,b>0).
(1)求f(x)的定义域;
(2)讨论f(x)的奇偶性;
(3)讨论f(x)的单调性.
已知定义域为R的函数f(x)为奇函数,且满足f(x+2)=-f(x),当x∈[0,1]时,f(x)=2x-1.
(1)求f(x)在[-1,0)上的解析式;
(2)求f(log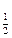 24).
24).
已知函数f(x)=loga(x+1)(a>1),若函数y=g(x)图象上任意一点P关于原点对称点Q的轨迹恰好是函数f(x)的图象.
(1)写出函数g(x)的解析式;
(2)当x∈[0,1)时总有f(x)+g(x)≥m成立,求m的取值范围.
已知函数f(x)=log2(x2-ax-a)在区间(-∞,1-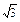 ]上是单调递减函数.求实数a的取值范围.
]上是单调递减函数.求实数a的取值范围.