已知定义在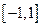 上的奇函数
上的奇函数 , 当
, 当 时,
时,  .
.
(1)求函数 在
在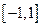 上的解析式;
上的解析式;
(2)试用函数单调性定义证明: 在
在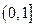 上是减函数;
上是减函数;
(3)要使方程 ,在
,在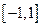 上恒有实数解,求实数
上恒有实数解,求实数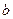 的取值范围.
的取值范围.
(本小题满分12分)
已知函数 ,且
,且 ,
, 。
。
(1)求函数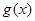 的解析式;(2)求函数
的解析式;(2)求函数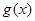 在
在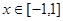 上的值域。
上的值域。
(本小题满分12分)
已知集合 ,
, ,若
,若 ,求实数
,求实数 的取值范围。
的取值范围。
(本小题16分)设双曲线: 的焦点为F1,F2.离心率为2。
的焦点为F1,F2.离心率为2。
(1)求此双曲线渐近线L1,L2的方程;
(2)若A,B分别为L1,L2上的动点,且2 ,求线段AB中点M的轨迹方程,并说明轨迹是什么曲线。
,求线段AB中点M的轨迹方程,并说明轨迹是什么曲线。
(本小题满分16分)
如图,在四棱锥 中,底面
中,底面 是矩形,
是矩形, 平面
平面 ,
, ,
, .以
.以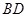 的中点
的中点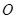 为球心、
为球心、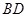 为直径的球面切
为直径的球面切 于点
于点 .
.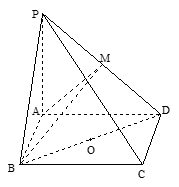
(1)求证:PD⊥平面 ;
;
(2)求直线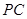 与平面
与平面 所成的角的正弦值;
所成的角的正弦值;
(3)求点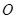 到平面
到平面 的距离.
的距离.
如图,直线l:y=x+b与抛物线C:x2=4y相切于点A.
(1)求实数b的值;
(2)求以点A为圆心,且与抛物线C的准线相切的圆的方程.