国庆60周年阅兵中,歼10飞机受阅后返回某机场,降落在跑道上减速过程简化为两个匀减速直线运动.飞机以速度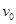 =100m/s着陆后立即打开减速阻力伞,加速度大小为
=100m/s着陆后立即打开减速阻力伞,加速度大小为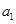 =5m/s2,运动时间为=10s;随后在无阻力伞情况下匀减速直至停下.在平直跑道上减速滑行总路程为
=5m/s2,运动时间为=10s;随后在无阻力伞情况下匀减速直至停下.在平直跑道上减速滑行总路程为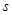 =1500m.求:第二个减速阶段飞机运动的加速度大小和时间.
=1500m.求:第二个减速阶段飞机运动的加速度大小和时间.
如图所示,重物重力G=20N,求OA、OB绳的拉力是多大?(要求作出力的示意图)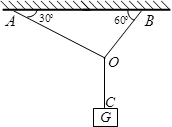
如图所示,一矩形绝缘木板放在光滑水平面上,另一质量为m、带电量为q的小物块沿木板上表面以某一初速度从A端沿水平方向滑入,木板周围空间存在足够大、方向竖直向下的匀强电场.已知物块与木板间有摩擦,物块沿木板运动到B端恰好相对静止.若将匀强电场的方向改为竖直向上,大小不变,且物块仍以原初速度沿木板上表面从A端滑入,结果物块运动到木板中点时相对静止.求: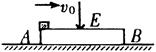
⑴物块所带电荷的性质.
⑵匀强电场场强的大小
质量m=2.0×10-4kg、电荷量q=1.0×10-6C的带正电微粒静止在空间范围足够大的匀强 电场中,电场强度大小为E1.在t=0时刻,电场强度突然增加到E2=4.0×103N/C,场强方向保持不变.到t=0.20s时刻再把电场方向改为水平向右,场强大小保持不变.取g=10m/s2.求:
电场中,电场强度大小为E1.在t=0时刻,电场强度突然增加到E2=4.0×103N/C,场强方向保持不变.到t=0.20s时刻再把电场方向改为水平向右,场强大小保持不变.取g=10m/s2.求:
(1)原来电场强度E1的大小?
(2)t=0.20s时刻带电微粒的速度大小?
(3)带电微粒运动速度水平向右时刻的动能?
一匀强电场,场强方向是水平的(如右图)。一个质量为m的带正电的小球,从O点出发,初速度的大小为v0,在电场力与重力的作用下,恰能沿与场强的反方向成θ角的直线运动。求小球运动到最高点时其电势能与在O点的电势能之差。