（本小题12分）
在某个以旅游业为主的地区，每年各个月份从事旅游服务工作的人数会发生周期性变化．现假设该地区每年各个月份从事旅游服务工作的人数
可近似地用函数
来刻画．其中：正整数
表示月份且
，例如
时表示1月份；
和
是正整数；
．
统计发现，该地区每年各个月份从事旅游服务工作的人数有以下规律：
①各年相同的月份，该地区从事旅游服务工作的人数基本相同；
②该地区从事旅游服务工作的人数最多的8月份和最少的2月份相差约400人；
③2月份该地区从事旅游服务工作的人数约为100人，随后逐月递增直到8月份达到最多．
（I）试根据已知信息，确定一个符合条件的的表达式；
（II）一般地，当该地区从事旅游服务工作的人数超过400人时，该地区进入了一年中的旅游“旺季”．那么，一年中的哪几个月是该地区的旅游“旺季”？请说明理由．
已知f(x)=
(a∈R)是R上的奇函数，
(1)求a的值；
(2)求f(x)的反函数f－1(x);
(3)对任意给定的k∈R+,解不等式f－1(x)>lg
.
已知f(x)是偶函数而且在(0，+∞)上是减函数，判断f(x)在(－∞,0)上的增减性并加以证明.
在Rt△ABC中，∠C=90°，以斜边AB所在直线为轴将△ABC旋转一周生成两个圆锥，设这两个圆锥的侧面积之积为S1，△ABC的内切圆面积为S2，记
=x.
(1)求函数f(x)=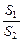
的解析式并求f(x)的定义域.
(2)求函数f(x)的最小值.
某家电生产企业根据市场调查分析，决定调整产品生产方案，准备每周(按120个工时计算)生产空调器、彩电、冰箱共360台，且冰箱至少生产60台.已知生产家电产品每台所需工时和每台产值如下表:
| 家电名称 |
空调器 |
彩电 |
冰箱 |
| 工时 |
 |
 |
 |
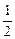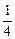| 产值(千元) |
4 |
3 |
2 |
问每周应生产空调器、彩电、冰箱各多少台，才能使产值最高？最高产值是多少？(以千元为单位)
已知函数f(x)=lg［(a2－1)x2+(a+1)x+1］
(1)若f(x)的定义域为(－∞,+∞)，求实数a的取值范围；
(2)若f(x)的值域为(－∞,+∞),求实数a的取值范围