．要将甲、乙两种长短不同的钢管截成A、B、C三种规格，每根钢管可同时截得三种规格的短钢管的根数如下表所示：
规格类型
|
A规格 |
B规格 |
C规格 |
||
| 甲种钢管 |
2 |
1 |
4 |
||
| 乙种钢管 |
2 |
3 |
1 |
今需A、B、C三种规格的钢管各13、16、18根，问各截这两种钢管多少根可得所需三种规格钢管，且使所用钢管根数
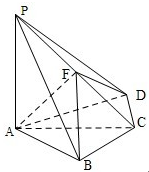
如图，四棱锥
中，
.
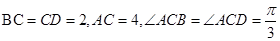,F为PC的中点，
.
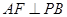（1）求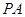
的长：
（2）求二面角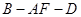
的正弦值.
（本小题满分12分）在一个盒子中，放有大小相同的红、白、黄三个小球，现从中任意摸出一球，若是红球记1分，白球记2分，黄球记3分．现从这个盒子中，有放回地先后摸出两球，所得分数分别记为
、
，设
为坐标原点，点
的坐标为
，记
．
（1）求随机变量
的最大值，并求事件“取得最大值”的概率；
（2）求随机变量的分布列和数学期望．
已知函数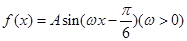
相邻两个对称轴之间的距离是
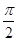，且满足，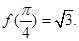
（1）求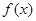
的单调递减区间；
（2）在钝角△ABC中，a、b、c分别为角A、B、C的对边，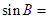
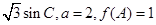,求△ABC的面积.
已知圆C：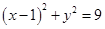
内有一点P（2，2），过点P作直线l交圆C于A、B两点.
（1）当弦AB被点P平分时，写出直线l的方程；
（2）当直线l的倾斜角为45º时，求弦AB的长.
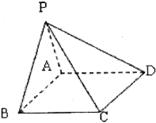
如图，在四棱锥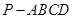
中，底面
是矩形，已知
，
（1）证明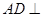
平面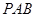
；
（2）求异面直线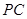
与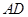
所成的角的正切值；
（3）求四棱锥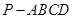的体积。