如图14-2-5所示电路中,L是电阻不计的线圈,C为电容器,R为电阻,开关S先是闭合的,现将开关S断开,并从这一时刻开始计时,设电容器A极板带正电时电荷量为正,则电容器A极板上的电荷量q随时间t变化的图象是图14-2-6中的( )
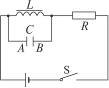
图14-2-5
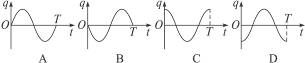
图14-2-6
如图所示,要使Q线圈产生图示方向的电流,可采用的方法有( )
| A.闭合电键K |
| B.闭合电键K后,把R的滑片右移 |
| C.闭合电键K后,把P中的铁心从左边抽出 |
| D.闭合电键K后,把Q靠近P |
如图所示的直流电路稳定运行,在水平放置的平行板电容器C两板间有一个带电液滴正好可以静止。下列哪些变化可能造成液滴下降( )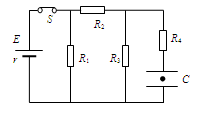
| A.开关S断开 |
| B.R4断路故障 |
| C.R2短路故障 |
| D.电容器上极板下降(不碰到液滴) |
一带电粒子在电场中只受电场力而运动,如图实线为电场线,虚线为粒子的轨迹,根据图像可以判定( )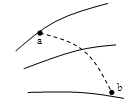
| A.a点的电势高于b点电势 |
| B.a点的电场强度强于b点 |
| C.粒子在a点的速度比b点大 |
| D.粒子在a点的电势能比b点大 |
关于电磁感应,下列说法不正确的有( )
A. 闭合回路中的磁通量变化时就有感应电流,停止变化感应电流就消失
B. 之所以会有感应电流是由于电路中产生了感应电动势,所以没有感应电流就说明没有感应电动势
C. 导体切割磁感线时会有电磁感应现象,其机理可由洛伦兹力解释
关于磁感应强度,下列说法正确的是( )
| A.同一段通电直导线,放到两个匀强磁场中,受到安培力大的磁感应强度大 |
| B.只有通过小磁针在磁场中的指向才能从实验上确定磁感应强度的方向 |
| C.磁感应强度是矢量,即使它不与通电导线垂直,仍可按平行四边形定则叠加 |
D.由公式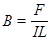 ,磁感应强度的国际单位是NA-1m-1 ,磁感应强度的国际单位是NA-1m-1 |