如图3-11所示,单匝线圈在匀强磁场中绕OO′轴从图示的位置开始匀速转动,已知从图示位置转过π/6时,线圈中的电动势大小为6 V,求: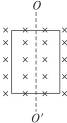
图3-11
(1)交变电动势的最大值、有效值;
(2)设线圈的电阻为R="1" Ω,角速度ω="100" rad/s,线圈由图示位置转过π/2的过程中通过导线截面的电荷量.
如图所示,一个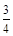 圆弧形光滑细圆管轨道ABC,放置在竖直平面内,轨道半径为R,在A点与水平地面AD相接,地面与圆心O等高,MN是放在水平地面上长为3R、厚度不计的垫子,左端M正好位于A点.将一个质量为m、直径略小于圆管直径的小球从A处管口正上方某处由静止释放,不考虑空气阻力.
圆弧形光滑细圆管轨道ABC,放置在竖直平面内,轨道半径为R,在A点与水平地面AD相接,地面与圆心O等高,MN是放在水平地面上长为3R、厚度不计的垫子,左端M正好位于A点.将一个质量为m、直径略小于圆管直径的小球从A处管口正上方某处由静止释放,不考虑空气阻力.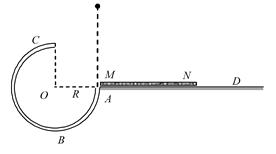
(1)若小球从C点射出后恰好能打到垫子的M端,则小球经过C点时对管的作用力大小和方向如何?
(2)欲使小球能通过C点落到垫子上,小球离A点的最大高度是多少?
轮滑运动员与滑轮总质量为M,运动员手托着一个质量为m的彩球,在半圆形轨道上及空中进行表演,如图所示。运动员从半圆轨道边缘a由静止开始下滑,冲上轨道另一边等高点b后继续竖直上升,到达最高点时立即竖直上抛手中的彩球。彩球从手中抛出到最高点时间t恰等于运动员离开b点运动到最高点时的时间。设在半圆形轨道运动过程中需要克服阻力做功为Wf,不计空气阻力。
求:(1)人抛出彩球时对彩球所做的功。
(2)人在圆形轨道中所做的功。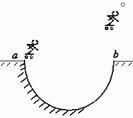
如图14所示,在同一竖直上,质量为2m的小球A静止在光滑斜面的底部,斜面高度为H=2L。小球受到弹簧的弹性力作用后,沿斜面向上运动。离开斜面后,运动到最高点时与静止悬挂在此处的小球B发生碰撞(碰撞过程无动能损失);碰撞后球B刚好能摆到与悬点O同一高度,球A沿水平方向抛射落在水平面C上的P点,O点的投影O'与P的距离为L/2。已知球B质量为m,悬绳长L,视两球为质点,重力加速度为g,不计空气阻力,求:
(1)球A在两球碰撞后一瞬间的速度大小;
(2)弹簧的弹性力对球A所做的功。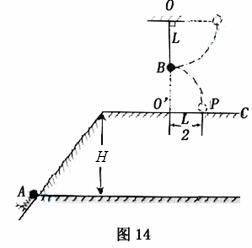
质量为m=2kg小球用长为L=2m的轻绳连接在天花板上的O点,如图所示,现将小球拉至图示位置静止释放,图示位置绳与竖直方向夹角θ=60°,由于绳能承受的张力有限,当小球摆到最低点时,绳子恰好被拉断。
最低点距地面高h=1.25m。(空气阻力不计, g=10m/s2)
(1)求小球运动到最低点的速度。
(2)求绳子能承受的最大拉力约为多少?
(3)求小球自静止释放到着地过程中的水平位移。
如图所示,在光滑的水平面上放着一个质量为M=0.39kg的木块(可视为质点),在木块正上方1m处有一个固定悬点O,在悬点O和木块之间连接一根长度为1m的轻绳(轻绳不可伸长)。有一颗质量为m = 0.01kg的子弹以400m/s的速度水平射入木块并留在其中,随后木块开始绕O点在竖直平面内做圆周运动。g取10m/s2。求:
(1)当木块刚离开水平面时的速度;
(2)当木块到达最高点时轻绳对木块的拉力多大?