如图所示,匝数为100、边长为 0.2 m的正方形线圈,在磁感应强度为2 T的匀强磁场中,从中性面开始以10π rad/s的角速度绕OO′轴匀速转动.若线圈自身电阻为2 Ω,负载电阻R="6" Ω,π2≈10,则开始转动 s内在电阻R上产生的热量为多少焦耳?
s内在电阻R上产生的热量为多少焦耳?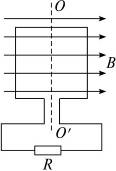
一皮带传动装置如图所示,皮带的速度v足够大.一根质量不计、劲度系数为k的弹簧一端固定,另一端连接一个质量为m的滑块,已知滑块与皮带间的动摩擦因数为μ.当滑块放到皮带上时,弹簧的轴线恰好水平,若滑块放到皮带上的瞬间,滑块的速度为零,且弹簧正好处于自由长度,则当弹簧第一次伸长到最大时,滑块与皮带间所产生的热量是多少?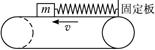
如图所示,abc为固定在水平面上的光滑圆弧轨道,b点为最低点,O为圆心,弧abc所对圆心角小于5°,现将甲球由O点、乙球由a点同时由静止释放(把两球视为质点),若不计空气阻力,哪个球先到达b点?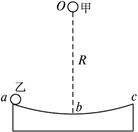
如图,长木板ab的b端固定一挡板,木板连同挡板的质量为M="4.0" kg,a、b间距离s="2.0" m.木板位于光滑水平面上.在木板a端有一小物块,其质量m="1.0" kg,小物块与木板间的动摩擦因数μ=0.10,它们都处于静止状态.现令小物块以初速v0="4.0" m/s 沿木板向前滑动,直到和挡板相碰.碰撞后,小物块恰好回到a端而不脱离木板.求碰撞过程中损失的机械能.
如图所示,EF为水平地面,O点左侧是粗糙的、右侧是光滑的.一轻质弹簧右端与墙壁固定,左端与静止在O点质量为m的小物块A连结,弹簧处于原长状态.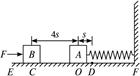
质量为m的物块B在大小为F的水平恒力作用下由C处从静止开始向右运动,已知物块B与地面EO段间的滑动摩擦力大小为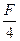 ,物块B运动到O点与物块A相碰并一起向右运动(设碰撞时间极短),运动到D点时撤去外力F.已知CO=4s,OD=s.求撤去外力后:
,物块B运动到O点与物块A相碰并一起向右运动(设碰撞时间极短),运动到D点时撤去外力F.已知CO=4s,OD=s.求撤去外力后:
(1)弹簧的最大弹性势能;
(2)物块B最终离O点的距离.
如图所示,带正电小球质量为m=1×10-2 kg,带电荷量为q=1×10-6 C,置于光滑绝缘水平面上的A点.当空间存在着斜向上的匀强电场时,该小球从静止开始始终沿水平面做匀加速直线运动,当运动到B点时,测得其速度vb="1.5" m/s,此时小球的位移为s="0.15" m.求此匀强电场场强E的取值范围.(g取10 m/s2)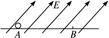
某同学求解如下:设电场方向与水平面之间夹角为θ,由动能定理qEscosθ=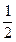 mvB2-0,得E=
mvB2-0,得E=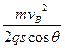 =
=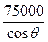 V/m,由题意可知θ>0,所以当E>7.5×104 V/m时小球将始终沿水平面做匀加速直线运动.
V/m,由题意可知θ>0,所以当E>7.5×104 V/m时小球将始终沿水平面做匀加速直线运动.
经检查,计算无误.该同学所得结论是否有不完善之处?若有请予以补充.