已知平面上一定点C（4，0）和一定直线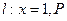
为该平面上一动点，作
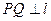，垂足为Q，且
.
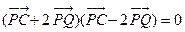（1）问点P在什么曲线上？并求出该曲线的方程；
（2）设直线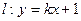
与（1）中的曲线交于不同的两点A、B，是否存在实数k，使得以线段AB为直径的圆经过点D（0，－2）？若存在，求出k的值，若不存在，说明理由.
已知数列
的前
项和为
，且
.
（1）证明：
是等比数列；
（2）求数列
的通项公式，并求出使得
成立的最小正整数.
等比数列
的前
项和为
，若
是
与
的等差中项，求数列的公比
的值.
甲、乙两物体分别从相距70m的两处同时相向运动.甲第一分钟走2m，以后每分钟比前一分钟多走1m，乙每分钟都是走5m.
（1）问：甲、乙开始运动后几分钟第一次相遇？
（2）如果甲、乙到达对方起点后立即折返，双方仍按原来的运动方式运动，那么从一开始运动后几分钟第二次相遇？
已知三个数成等差数列，它们的和为15，如果它们分别加上1，3，9就成等比数列，求这三个数.
数列{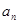
}是首项为23，公差为 -4的等差数列.
（1）当
时，求
的取值范围.
（2）求
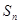的最大值.