如图13-8-3所示,一水平放置的圆盘绕竖直固定轴转动,在圆盘上沿半径开有一条宽度为2 mm的均匀狭缝.将激光器与传感器上下对准,使二者间连线与转轴平行,分别置于圆盘的上下两侧,且可以同步地沿圆盘半径方向匀速移动,激光器连续向下发射激光束.在圆盘转动过程中,当狭缝经过激光器与传感器之间时,传感器接收到一个激光信号,并将其输入计算机,经处理后画出相应图线.图(a)为该装置示意图,图(b)为所接收的光信号随时间变化的图线,横坐标表示时间,纵坐标表示接收到的激光信号强度,图中Δt1=1.0×10-3 s,Δt2=0.8×10-3 s.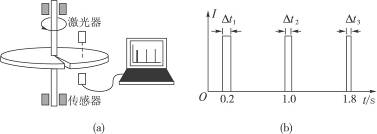
图13-8-3
(1)利用图(b)中的数据求1 s时圆盘转动的角速度;
(2)说明激光器和传感器沿半径移动的方向;
(3)求图(b)中第三个激光信号的宽度Δt3.
在离水平地面45 m的高处以10 m/s的初速度沿水平方向抛出一个质量为0.5 kg的小球,不计空气阻力,求:
(1)在第1 s内、第2 s内、第3 s内重力势能的改变量之比ΔEp1∶ΔEp2∶ΔEp3是多少?
(2)在第1 s内、第2 s内、第3 s内的动能变化量之比ΔEk1∶ΔEk2∶ΔEk3是多少?
(3)设物体在地面上的重力势能为零,在什么高度处重力势能和动能相等?(取g="10" m/s2)
如图7-5-13所示,底面积为2a2的两个圆柱形容器,底部用细管连接,左边容器的水面浮着一个边长为a的正方形木块,木块的一半浸在水中.现将木块慢慢提出水面,则容器中水的重力势能减少了.
图7-5-13
有一上端挂在墙上的长画,从画的上端到下面的画轴长1.8 m,下面画轴重1 N,画重0.8 N(画面处处均匀),现将长画从下向上卷起来,求长画的重力势能增加了多少.
如右图所示,一根不可伸长的轻质细线,一端固定于O点,另一端拴有一质量为m的小球,可在竖直平面内绕O点摆动.现拉紧细线使小球位于与O点在同一竖直面内的A位置,细线与水平方向成30°角,从静止释放该小球,当小球运动至悬点正下方C位置时,细线承受的拉力是多大?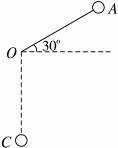
盘在地面上的一根不均匀的金属链重30 N,长1 m,从一端缓慢提起至另一端恰好离开地面时需做功10 J,金属链重力势能增加多少?此时金属链重心位置距地面多高?如果改从另一端缓慢提起至金属链恰好离开地面需做功多少?