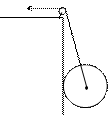
一半圆形玻璃砖,玻璃的折射率为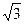 ,AB为其直径,长度为D,O为圆心.一束宽度恰等于玻璃砖半径的单色平行光束垂直于AB从空气射入玻璃砖,其中心光线P通过O点,如图19-2-17所示.M、N为光束边界光线.则M、N射出玻璃砖后的相交点距O点的距离为多少?
,AB为其直径,长度为D,O为圆心.一束宽度恰等于玻璃砖半径的单色平行光束垂直于AB从空气射入玻璃砖,其中心光线P通过O点,如图19-2-17所示.M、N为光束边界光线.则M、N射出玻璃砖后的相交点距O点的距离为多少?
图19-2-17
(1)飞船垂直地面发射升空,在加速上升过程中宇航员处于超重状态,人们把这种状态下飞船的视重与静止在地球表面时飞船的重力的比值称为耐受力值,用K表示。若飞船发射时加速度的变化范围是20m/s2≤a≤100m/s2,则宇航员的耐受力值范围是多少?
(2)“神舟”五号飞船返回舱降到距地面约10km时,回收着陆系统启动工作,设经过一段时间后,在临近地面时降落伞使返回舱以7.0m/s的速度匀速竖直下降。在距地面约1.0m时,返回舱的4个相同的反推火箭发动机同时点火工作,使返回舱以不大于3.0m/s的速度接触地面,实现软着陆。若返回舱的质量约为2.7t ,求一个反推火箭发动机产生的推力至少是多大?
一物体作匀加速直线运动,在2s内通过的位移为6m,在紧接着的1s内通过的位移也为6m。求物体运动的加速度的大小。