某同学在测定一厚度均匀的圆形玻璃的折射率时,先在白纸上作一与圆形玻璃同半径的圆,圆心为O,将圆形玻璃平放在白纸上,使其边界与所画的圆重合.在玻璃一侧竖直插两枚大头针P1和P2.在另一侧再先后插两枚大头针P3和P4,使从另一侧隔着玻璃观察时,大头针P4、P3和P2、P1的像恰在一直线上.移去圆形玻璃和大头针后,在图13-1-24中画出:
图13-1-24
(1)沿P1、P2连线方向的入射光线通过圆形玻璃后的传播方向;
(2)光线在玻璃内的传播方向;
(3)过光线的入射点作法线,标出入射角θ1和折射角θ2;
(4)写出计算玻璃折射率的公式.
如图所示,竖直放置的半圆形绝缘光滑轨道半径R=40cm,下端与绝缘光滑的水平面平滑连接,整个装置处于方向竖直向下,大小为E=1×103V/m的匀强电场中,一质量为m=10g、带电量为q=+1×10-4C的小物块(可视为质点),从水平面上的A点以初速度v0水平向左运动,沿半圆形轨道恰好能通过最高点C,取g=10m/s2,试求:
(1)小物块从C点抛出后落地点与B点间的水平距离;
(2)v0的大小和过B点时轨道对小物块的支持力大小;
一灵敏电流计,允许通过的最大电流(满刻度电流)为Ig=50μA,表头电阻Rg=1kΩ
(1)若改装成量程为Im=1mA的电流表,应该串联还是并联一个电阻? 新表内阻为多少?
(2)若将改装后的电流表再改装成量程为Um=10V的电压表,应该再串联还是并联一个多大的电阻?
如图所示的匀强电场中,有a、b、c三点,ab间距离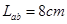 ,bc间距离
,bc间距离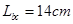 ,其中ab沿电场方向,bc和电场方向成60°角.一个所带电量
,其中ab沿电场方向,bc和电场方向成60°角.一个所带电量 的负电荷从a点移到b点克服电场力做功
的负电荷从a点移到b点克服电场力做功 .求:
.求:
(1)匀强电场的电场强度;
(2)电荷从b点移到c点,电场力所做的功;
(3)a、c两点间的电势差.
一台小型电动机在3V电压下工作,通过它的电流是0.2A,用此电动机提升物重4N的物体,在30秒内可以使该物体匀速提升3m,除电动机线圈生热之外不计其它的能量损失,求
(1)电动机的输入电功率。
(2)在提升重物的30秒内,电动机线圈所产生的热量。
(3)线圈的电阻。
质谱仪是一种测定带电粒子质量和分析同位素的重要工具,它的构造如图所示。设离子源S产生离子,离子产生出来时速度很小,可以看作速度为零。产生的离子经过电压为U的电场加速后(图中未画出),进入一平行板电容器C中,电场E和磁场B1相互垂直,具有某一速度的离子将沿图中虚直线穿过两板间的空间而不发生偏转,而具有其他速度的离子发生偏转。最后离子再进入磁感应强度为B2的匀强磁场,沿着半圆周运动,到达记录它的照相底片上的P点,根据以上材料回答下列问题:
(1)证明能穿过平行板电容器C的离子具有的速度为v=E/B1
(2)若测到P点到入口S1的距离为x,证明离子的质量m=qB22x2/8U