已知A、B是抛物线y2=2px(p>0)上的两点,且满足OA⊥OB(O为坐标原点).
求证:(1)A、B两点的横坐标之积、纵坐标之积分别为定值;(2)直线AB经过一个定点.
求函数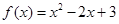 在下列定义域内的值域。
在下列定义域内的值域。
(1)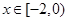 函数y=f(x)的值域
函数y=f(x)的值域
(2)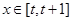 (其中
(其中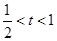 )函数y=f(x)的值域。
)函数y=f(x)的值域。
集合A={x|x2-ax+a2-19=0},B={x|x2-5x+6=0},
C={x|x2+2x-8=0}.
(1)若A∩B=A∪B,求a的值;
(2)若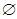
 A∩B,A∩C=
A∩B,A∩C=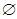 ,求a的值.
,求a的值.
在极坐标系中,圆ρ=2cosθ与直线3ρcosθ+4ρsinθ+a=0相切,求实数a的值
设函数f(x)=(1+x)2-2ln (1+x).
(1)求函数f(x)的单调区间;
(2)若关于x的方程f(x)=x2+x+a在[0,2]上恰有两个相异实根,求实数a的取值范围.
现需要制作一个容积为32 的有铝合金盖的圆柱形铁桶,已知单位面积铝合金的价格是铁的3倍,问底面半径多大时桶的总造价最小?
的有铝合金盖的圆柱形铁桶,已知单位面积铝合金的价格是铁的3倍,问底面半径多大时桶的总造价最小?