在平面向量中有如下定理：设点O，P，Q，R为同一平面内的点，则P、Q、R三点共线的充要条件是：存在实数t，使
.
如图，在ΔABC中，点E为AB边的中点，点F在AC边上，
且CF＝2FA，BF交CE于点M，设
，则
A． |
B． |
C． |
D． |
已知点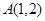
、
，则线段
的垂直平分线的方程是（）
A． |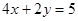
B． |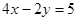
C． |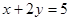
D． |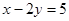
下列说法不正确的是（）
| A．空间中，一组对边平行且相等的四边形是一定是平行四边形； |
| B．同一平面的两条垂线一定共面； |
| C．过直线上一点可以作无数条直线与这条直线垂直，且这些直线都在同一个平面内； |
| D．过一条直线有且只有一个平面与已知平面垂直. |
过点
且平行于直线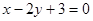
的直线方程为（）
A． |
B． |
C． |
D． |
已知直线经过点A(0,4)和点B（1，2），则直线AB的斜率为（）
| A．3 | B．-2 | C．2 | D．不存在 |
下图表示某人的体重与年龄的关系，则( )
| A．体重随年龄的增长而增加 |
| B．25岁之后体重不变 |
| C．体重增加最快的是15岁至25岁 |
| D．体重增加最快的是15岁之前 |
