如图6-1-9所示,一物体从光滑斜面顶端由静止开始下滑.已知物体的质量m="0.50" kg,斜面的倾角θ=30°,斜面长度L="2.5" m,重力加速度取g="10" m/s2.求:
图6-1-9
(1)物体沿斜面下滑的加速度大小;
(2)物体滑到斜面底端时的速度大小;
(3)物体下滑的全过程中重力对物体的冲量大小.
如图所示,C是放在光滑的水平面上的一块木板,木板的质量为3m,在木板的上面有两块质量均为m的小木块A和B,它们与木板间的动摩擦因数均为μ。最初木板静止,A、B两木块同时以方向水平向右的初速度V0和2V0在木板上滑动,木板足够长, A、B始终未滑离木板。求:
(1)木块B从刚开始运动到与木板C速度刚好相等的过程中,木块B所发生的位移;
(2)木块A在整个过程中的最小速度。
甲、乙两小孩各乘一辆小车在光滑水平面上匀速相向行驶,速度均为6m/s。甲车上有质量为m=1kg的小球若干个,甲和他的车及所带小球的总质量为M1=50kg,乙和他的车总质量为M2=30kg。现为避免相撞,甲不断地将小球以相对地面16.5m/s的水平速度抛向乙,且被乙接住。假设某一次甲将小球抛出且被乙接住后刚好可保证两车不致相撞,试求此时:
(1)两车的共同速度为多少?(2)甲总共抛出了多少个小球?
质量为M、长为L的船静止在静水中,船头及船尾各站着质量分别为m1及m2的人,当两人互换位置后,船的位移有多大?
如图所示,光滑水平面上有A、B两小车,质量分别为 mA=20㎏,mB=25㎏。以初速度v0=3m/s向右运动,B车原静止,且B车右端放着物块C,C的质量为 mC=15㎏。A、B相撞且在极短时间内连接在一起,不再分开。已知C与B水平表面间动摩擦因数为μ=0.20,B车足够长,求C沿B上表面滑行的长度。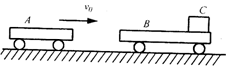
如图所示,在光滑水平桌面上,物体A和B用轻弹簧连接,另一物体C靠在B左侧未连接,它们的质量分别为mA=0.2kg,mB=mC=0.1kg。现用外力将B、C和A压缩弹簧,外力做功为7.2J,弹簧仍在弹性限度内然后由静止释放。试求:
弹簧伸长最大时弹簧的弹性势能;
弹簧从伸长最大回复到自然长度时,A、B速度的大小。