如图8-8-10所示，两块大小不同、质量分别为M和m的圆形薄板（厚度不计），半径分别为R和r，M=3m，两板之间用一根长为L="0.40" m的轻绳相连接.开始时，两板水平放置并叠合在一起处于静止状态，在其正下方0.80 m处有一固定支架C，支架上有一半径为R′(r＜R′＜R)的圆孔，圆孔与两薄板中心均在圆孔中心轴线上.今使两板一起自由下落，空气阻力不计，大板与支架C发生没有机械能损失的弹性碰撞，碰撞后两板即分离，直到轻绳绷紧，在轻绳绷紧的瞬间，两板便获得共同速度，g取10 m/s2.试求这个共同速度的大小.
如图所示，A、B两物体相互接触并同时由静止开始沿斜面匀加速滑下．设它们的质量分别为
，它们与斜面之间的动摩擦因数为
，斜面倾角为
．试求滑下过程中A、B之间的相互作用力，并指出在什么条件下相互间无作用力，在什么条件下，二物体下滑时将分开?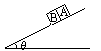
如图所示，质量为m的物体放在倾角为
的斜面上，物体与斜面间的动摩擦因数为μ，若沿斜面向上施一力F1或沿水平方向施一力
能使物体产生相同的加速度，其加速度大小为a，求
∶＝?
假设一质量为250kg的赛艇在水中航行时受到的总阻力与它的速度成正比，赛艇以恒定牵引力由静止开始加速，当赛艇速度达到5m/s时，其加速度恰为4m/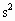
．已知赛艇在这一恒定牵引力作用下所能达到的最大速度是10m/s，试求赛艇这一恒定牵引力是多大？
某物体以一定的初速率沿斜面向上运动，设物体沿斜面运动的最大位移为
，由实验测得与斜面倾角
的关系如图所示，试求：
(1)物体沿斜面上升的初速；
(2)物体与斜面间的动摩擦因数；
(3)物体沿斜面运动的位移最小时斜面的倾角．
某星球半径为R，在这个星球表面以初速
竖直上抛一个物体，没有空气阻力的影响，经过t秒钟落向地面．
(1)这个星球表面处的重力加速度g是多大?
(2)要在这个星球上发射一个环绕近地轨道做匀速圆周运动的卫星，卫星的速度是多大?