如图所示,光滑水平面上有一辆质量为m的小车,车上左右两端分别站着甲、乙两人,他们的质量都是m,开始两个人和车一起以速度v0向右匀速运动。某一时刻,站在车右端的乙先以相对地面水平向右的速度v1跳离小车,然后站在车左端的甲以相对于地面水平向左的速度v1跳离小车,两人都离开小车后,小车的速度将是( )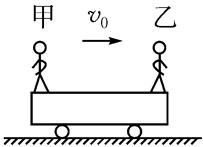
| A.v0 | B.2v0 | C.大于v0小于2v0 | D.大于2v0 |
2007年,诺贝尔物理学奖授予了发现巨磁电阻效应(GMR)的科学家.如图所示是研究巨磁电阻特性的原理示意图,已知该GMR磁性材料随着磁场增强电阻显著减小,那么,当闭合左图中S后使滑片向左滑动过程中,下图中电流表和电压表的读数变化情况是()
| A.电压表示数变小,电流表示数变大 |
| B.电压表示数变大,电流表示数变小 |
| C.电压表示数变小,电流表示数变小 |
| D.电压表示数变大,电流表示数变大 |
某 同学研究电子在电场中的运动时,电子仅受电场力作用,得到了电子由a点运动到b 点的轨迹(虚线所示)图中一组平行实线可能是电场线,也可能是等势面,则下列说法正确的是 ()
同学研究电子在电场中的运动时,电子仅受电场力作用,得到了电子由a点运动到b 点的轨迹(虚线所示)图中一组平行实线可能是电场线,也可能是等势面,则下列说法正确的是 ()
A.不论图中实线是 电场线还是等势面,a点的电势都比b 点低 电场线还是等势面,a点的电势都比b 点低 |
| B.不论图中实线是电场线还是等势面,a 点的场强都比b 点小 |
| C.如果图中实线是电场线,电子在a 点动能较小 |
| D.如果图中实线是等势面,电子在b点动能较小 |
如图所示,赤道上 随地球自转的物体A、赤道上空的近地卫星B、地球同步卫星C,它们的运动都可视为匀速圆周运动,比较三个物体的运动情况, 以下判断正确的是()
随地球自转的物体A、赤道上空的近地卫星B、地球同步卫星C,它们的运动都可视为匀速圆周运动,比较三个物体的运动情况, 以下判断正确的是()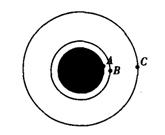
A.三者的周期关系为TA<TB<TC
B.三者向心加速度大小关系为aA>aB>aC
C.三者角速度的大小关系为ωA=ωC<ωB
D.三者线速度的大小关系为VA<VC<VB
构建和谐、节约型社会深得民心,这体现于生活的方方面面,自动充电式电动车就是很好的一例.在电动车的前轮处装有发电机,发电机与蓄电池连接.当骑车者用力蹬车或电动自行车自动滑行时,自行车就可以连通发电机对蓄电池充电,将其它形式的能转化成电能储存起来.某人骑车以500 J的初动能在粗糙的水平面上滑行,第一次关闭自动充电装置让车自由滑行,其动能随位移变化的关系如图线①所示;第二次启动自动充电装置,其动能随位移变化的关系如图线②所示.设两种情况下自行车受到的阻力(包括空气阻力和摩擦阻力等)恒定不变,则下列说法中正确的是()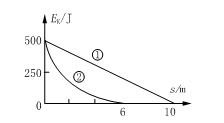
| A.自行车受到的阻力为50N |
| B.自行车受到的阻力约为83N |
| C.第二次向蓄电池所充的电能是200J |
| D.第二次向蓄电池所充的电能是250J |
用与竖直方向成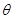 的倾斜绳子a和水平轻绳子b共同固定一个小球,这时绳b的拉力为F1。现在保持小球在原位置不动,使绳子b在原竖直平面内,逆时针转过
的倾斜绳子a和水平轻绳子b共同固定一个小球,这时绳b的拉力为F1。现在保持小球在原位置不动,使绳子b在原竖直平面内,逆时针转过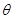 角固定,绳b的拉力变为F2;再转过
角固定,绳b的拉力变为F2;再转过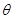 角固定,绳子b拉力变为F3,如图所示。则( )
角固定,绳子b拉力变为F3,如图所示。则( )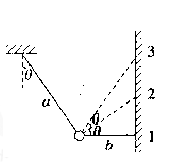
A.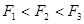 |
B.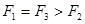 |
C. |
D.绳a拉力减小 |