如图16-11所示，abc是光滑的轨道，其中ab是水平的，bc为与ab相切的位于竖直平面内的半圆，半径R="0.30" m.质量m="0.20" kg的小球A静止在轨道上，另一质量M="0.60" kg、速度v0="5.5" m/s的小球B与小球A正碰.已知相碰后小球A经过半圆的最高点c落到轨道上距b点为l=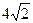
R处，重力加速度取g="10" m/s2.求：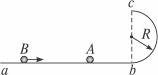
图16-11
(1)碰撞结束时，小球A和B的速度的大小.
(2)试论证小球B是否能沿着半圆轨道到达c点.
如图12所示，一束电荷量为e的电子以垂直于磁感应强度B并垂直于磁 场边界的速度v射入宽度为d的匀强磁场中，穿出磁场时速度方向和原来射入方向的夹角为θ=600。求穿越磁场的轨道半径、电子的质量和穿越磁场的时间。
如图所示，水平放置的两块长直平行金属板a、b相距d=0.10m，a、b间的电场强度为E=5.0×105N/C，b板下方整个空间存在着磁感应强度大小为B=6.0T、方向垂直纸面向里的匀强磁场.今有一质量为m=4.8×10-25kg、电荷量为q=1.6×10-18C的带正电的粒子(不计重力)，从贴近a板的左端以v0 =1.0×106m/s的初速度水平射入匀强电场，刚好从狭缝P处穿过b板而垂直进入匀强磁场，最后粒子回到b板的Q处(图中未画出).求P、Q之间的距离L.
在倾角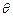
=30°的斜面上，固定一金属框，宽l=0.25m，接入电动势E=12V、内阻不计的电池．垂直框面放有一根质量m=0.2kg的金属棒ab，它与框架的动摩擦因数为
，整个装置放在磁感应强度B＝0.8T的垂直框面向上的匀强磁场中（如图11.2-５）．当调节滑动变阻器R的阻值在什么范围内时，可使金属棒静止在框架上？（设最大静摩擦力等于滑动摩擦力，框架与棒的电阻不计，g＝10m/s2）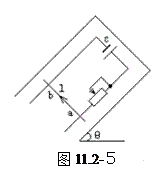
如图9所示，一束电子（电荷量为e）以速度v垂直射入磁感应强度为B，宽为d的匀强磁场中，穿过磁场时速度方向与电子原来入射方向的夹角为300，求：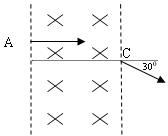
（1）电子的质量；
|
（2）电子穿过磁场所用的时间。
如图所示，半径为r的圆形空间内，存在着垂直于纸面向里的匀强磁场，一个带电粒子（不计重力），从A点以速度v0垂直磁场方向射入磁场中，并从B点射出，已知∠AOB=120°，求该带电粒子在磁场中运动的时间。(10分)