如右图所示,在倾角为37°的斜面上,固定着宽L="0.25" m的平行金属导轨,在导轨上端接入电源和变阻器.电源电动势E="12" V,内电阻r="1.0" Ω.一质量m="20" g的金属棒ab与两导轨垂直并接触良好,导轨与金属棒的电阻不计,整个装置处于磁感应强度B="0.80" T、垂直于斜面向上的匀强磁场中.若金属导轨是光滑的,取g="10" m/s2,且已知sin37°=0.60,cos37°=0.80.要保持金属棒静止在导轨上.求: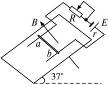
(1)回路中电流的大小;
(2)滑动变阻器接入电路的阻值.
“在测定某金属块的比热容时,先把质量已知的金属块放在沸水中加热.经过一段时间后把它迅速放进质量、温度均已知的水中,并用温度计测量水的温度.当水温不再上升时,这就是金属块与水的共同温度.根据实验数据就可以计算出金属块的比热容.”
以上叙述中,哪些地方涉及到了“平衡态”和“热平衡”的概念.
对于某体积不变的理想气体,温度每升高1℃,压强就增大了t0℃时物体压强的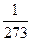 ,设t0℃时物体压强为p0,则温度为t时,物体压强为多少?(用两种方式表示)
,设t0℃时物体压强为p0,则温度为t时,物体压强为多少?(用两种方式表示)
利用油膜法可以粗略测出阿伏加德罗常数.把密度ρ=0.8×103 kg/m3的某种油,用滴管滴出一滴在水面上形成油膜,已知这滴油的体积为V=0.5×10-3 cm3,形成油膜面积为S="0.7" m2,油的摩尔质量M0="0.09" kg/mol.若把油膜看成是单分子层,每个油分子看成球形,那么:
(1)油分子的直径是多少?
(2)由以上数据可粗略测出阿伏加德罗常数NA是多少?先列出文字计算式,再代入数据计算.(只要求保留一位有效数字)
英国天文学家琴斯举过一个生动的例子来说明阿伏加德罗常数是一个十分巨大的数目.他说:“假定美国首任总统华盛顿临终时最后呼出的一口气至今均匀地散布在整个大气层中,那么我们每一个人的肺里可有好几个华盛顿最后一口气放出的分子.”设人的一次呼吸量大约是500 cm3,肺活量为2—3 L,地球半径为6 370 km.估算一下琴斯的说法是否正确?设大气层厚度为20 km.
用长度能放大600倍的显微镜观察布朗运动.估计放大后的小颗粒(碳粒)体积为0.1×10-9 m3,已知碳的密度是2.25×103 kg/m3,摩尔质量是1.2×10-2 kg/mol,阿伏加德罗常数为6.0×1023 mol-1,试估算小碳粒中的分子数和碳原子的直径.