在倾角θ=30°的斜面上,固定一金属框,宽l="0.25" m,接入电动势E="12" V、内阻不计的电池.垂直框的两对边放有一根质量m="0.2" kg的金属棒ab,它与框架的动摩擦因数μ=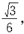 整个装置放在磁感应强度B="0.8" T、垂直框面向上的匀强磁场中,如图所示.当调滑动变阻器R的阻值在什么范围内,可使金属棒静止在框架上?框架与棒的电阻不计,g取10 m/s2
整个装置放在磁感应强度B="0.8" T、垂直框面向上的匀强磁场中,如图所示.当调滑动变阻器R的阻值在什么范围内,可使金属棒静止在框架上?框架与棒的电阻不计,g取10 m/s2
图11
如图所示是一种悬球式加速度仪,它可以用来测定沿水平轨道运动的列车的加速度,m是一个金属球,它系在金属丝的下端,金属丝的上端悬挂在O点,AB是一根长为l的电阻丝,其阻值为R。金属丝与电阻丝接触良好,摩擦不计,电阻丝的中点C焊接一根导线。从O点引出一根导线,两线之间
接入一个电压表V(金属丝和导线电阻不计),图中虚
线OC与AB相垂直,且OC=h,电阻丝AB接在电压
为U的直流稳压电源上,整个装置固定在列车中使A
B沿着车前进的方向,列车静止时金属丝呈竖直方向,
从电压表的读数变化可以测出加速度的大小。当列车向右做匀加速运动时,试写出加速度a与电压表读数U的对应关系,以便重新刻制电压表表面使它成为直读加速度数值的加速度计。
为什么C点设置在电阻丝AB的中间?对电压表的选择应有什么特殊要求?
把晶体二极管D和电阻R串联起来,连接成如图(a)的电路,电源的电动势E=5.0V,内阻不计,二极管两端电压U与其中的电流I的关系曲线(伏安特性曲线)如图(b),但为简单起见,可近似地看作直线,直线与横轴的交点EO=1V (见(b)图中的虚线),即二极管上所加电压U<EO时电流为零,U>EO时,I和U为线性关系,此二极管消耗的电功率超过4.0W时将被烧坏.试问:
电阻R最小要多大才不致烧坏二极管?
在保证不致烧坏二极管的条件下R值为多大时,输入给R的功率为最大?此功率最大值等于多少瓦?
风能将成为21世纪大规模开发的一种可再生清洁能源。风力发电机是将风能(气流的功能)转化为电能的装置,其主要部件包括风轮机、齿轮箱,发电机等。如图所示.
风轮机叶片旋转所扫过的面积为风力发电机可接受风能的面积。
设空气密度为p,气流速度为v,风轮机叶片长度为r。求单位时间内流向风轮机的最大风能Pm;在风速和叶片数确定的情况下,要提高风轮机单位时间接受的风能,简述可采取的措施。已知风力发电机的输出电功率P与Pm成正比。某风力发电机的风速v19m/s时能够输出电功率P1=540kW。我国某地区风速不低于v2=6m/s的时间每年约为5000小时,试估算这台风力发电机在该地区的最小年发电量是多少千瓦时。
如图所示,沿水平方向放置一条平直光滑槽,它垂直穿过开有小孔的两平行薄板,板相距3.5L。槽内有两个质量均为m的小球A和B,球A带电量为+2q,球B带电量为-3q,两球由长为2L的轻杆相连,组成一带电系统。最初A和B分别静止于左板的两侧,离板的距离均为L。若视小球为质点,不计轻杆的质量,在两板间加上与槽平行向右的匀强电场E后(设槽和轻杆由特殊绝缘材料制成,不影响电场的分布),求:
球B刚进入电场时,带电系统的速度大小;
带电系统从开始运动到速度第一次为零所需的时间及球A相对右板的位置。
在光滑的水平轨道上有两个半径都是r的小球A和B,质量分别为m和2m,如图2-6所示,当两球心间的距离大于L(L比2r大的多)时,两球间不存在相互作用力;当两球心间的距离等于或小于L时,两球间存在相互作用的恒定斥力F,现A球从远离B球处以速度V0沿两球心连接向原来静止的B球运动,欲时两球不发生接触,V0必须满足的条件?