已知函数
f(x)=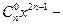
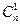
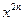
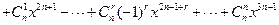 ,其中n
,其中n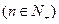 .
.
(1)求函数f(x)的极大值和极小值; (2)设函数f(x)取得极大值时x=
(2)设函数f(x)取得极大值时x=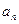 ,令
,令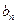 =2
=2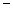 3
3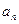 ,
,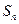 =
=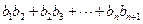 ,若p≤
,若p≤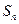 <q对一切n∈N+恒成立,求实数p和q的取值范围.
<q对一切n∈N+恒成立,求实数p和q的取值范围.
已知函数
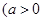 且
且 。(1)求函数
。(1)求函数 的定义域;(2)若函数
的定义域;(2)若函数 的最小值为
的最小值为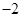 ,求实数
,求实数 的值。
的值。
已知数列 满足:
满足: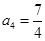 ,点
,点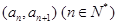 在直线
在直线 上,数列
上,数列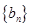 满足:
满足: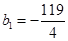 且
且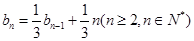 .
.
(I)求 的通项公式;
的通项公式;
(II)求证:数列 为等比数列;
为等比数列;
(3)求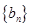 的通项公式;并探求数列
的通项公式;并探求数列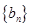 的前
的前 和的最小值
和的最小值
某新设备M在第1年可以生产价值120万元的产品,在使用过程中,由于设备老化及维修原因使得M的生产能力逐年减少,从第2年到第6年,每年M生产的产品价值比上年减少10万元;从第7年开始,每年M生产的产品价值为上年的75%.
(I)求第n年M生产的产品价值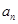 的表达式;
的表达式;
(II)该设备M从购买回来后马上使用,则连续正常使用10年可以生产多少价值的产品?
设命题
 成立;命题
成立;命题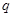 :
: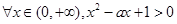 成立,如果命题
成立,如果命题 或
或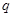 为真命题,命题
为真命题,命题 且
且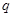 为假命题,求
为假命题,求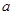 的取值范围。
的取值范围。
在 中,角
中,角 所对的边分别为
所对的边分别为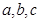 ,设
,设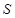 为
为 的面积,满足
的面积,满足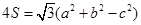
(I)求角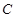 的大小;(II)若边长
的大小;(II)若边长 ,求
,求 的周长的最大值.
的周长的最大值.