从分别写有0,1,2,3,4,5,6的七张卡片中,任取4张,组成没有重复数字的四位数,计算:
(1)这个四位数是偶数的概率;
(2)这个四位数能被9整除的概率;
(3)这个四位数比4510大的概率。
已知关于x的方程: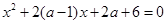 ,
,
(1)若方程有两个实根,求实数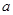 的范围;
的范围;
(2)设函数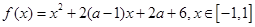 ,记此函数的最大值为
,记此函数的最大值为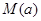 ,最小值为
,最小值为 ,求
,求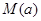 、
、 的解析式
的解析式
假设关于某设备的使用年限x和所支出的维修费用y (万元),有如下的统计数据 由资料知两变量呈线性相关,并且统计得五组数据的平均值分别为
由资料知两变量呈线性相关,并且统计得五组数据的平均值分别为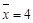 ,
, ,若用五组数据得到的线性回归方程
,若用五组数据得到的线性回归方程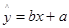 去估计,使用8年的维修费用比使用7年的维修费用多1.1万元,
去估计,使用8年的维修费用比使用7年的维修费用多1.1万元,
(1)求回归直线方程;
(2)估计使用年限为10年时,维修费用是多少?
某射手在一次射击中射中10环、9环、8环、7环、7环以下的概率分别为0.24、0.28、0.19、0.16、0.13.计算这个射手在一次射击中:
(1)至少射中7环的概率;
(2)射中环数不足8环的概率.
设集合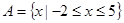 ,
,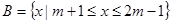 .
.
(Ⅰ) 若 ,求实数
,求实数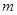 的取值范围;
的取值范围;
(Ⅱ) 当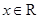 时,不存在元素
时,不存在元素 使
使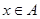 与
与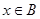 同时成立,求实数
同时成立,求实数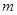 的取值范围.
的取值范围.
已知抛物线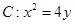 的焦点为
的焦点为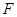 ,过点
,过点 的直线
的直线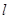 与
与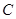 相交于
相交于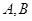 两点,点
两点,点 关于
关于 轴的对称点为
轴的对称点为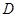 .
.
(Ⅰ)证明:点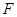 在直线
在直线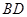 上;
上;
(Ⅱ)设 ,求
,求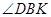 的平分线与
的平分线与 轴的交点坐标.
轴的交点坐标.